
【题目】如图,要得到DG∥BC,则需要条件( )
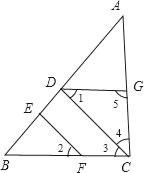
A. CD⊥AB,EF⊥AB B. ∠1=∠2
C. ∠1=∠2,∠4+∠5=180° D. CD⊥AB,EF⊥AB,∠1=∠2
【答案】D
【解析】分析:假设DG∥BC,则∠1=∠3,∠4+∠5+∠3=180°,再通过EF,CD之间的关系,确定∠2与∠3以及∠1与∠2的关系.
详解:A.∵CD⊥AB,EF⊥AB,∴∠BEF=∠BDC=90°,∴EF∥DC,故条件不充分,错误;
B.∠1与∠2不是DG与BC形成的内错角,故推不出DG∥BC,故错误;
C.∠1与∠2不是DG与BC形成的内错角,∠4与∠5不是DG与BC形成的同旁内角,故推不出DG∥BC,故错误;
D.当DG∥BC时,则∠1=∠3,当EF∥DC时,∠2=∠3,要使EF∥DC,则需CD⊥AB,EF⊥AB,所以要使DG∥BC,则需要CD⊥AB,EF⊥AB,同时∠1=∠2.
故选D.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
(1)填空:a= ,b= ,c= ;
(2)先化简,再求值:5a2b﹣[2a2b﹣3(2abc﹣a2b)]+4abc.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴分别交于点A、B,与y轴交于点C,且OA=1,OB=3,顶点为D,对称轴交x轴于点Q.

(1)求抛物线对应的二次函数的表达式;
(2)点P是抛物线的对称轴上一点,以点P为圆心的圆经过A、B两点,且与直线CD相切,求点P的坐标;
(3)在抛物线的对称轴上是否存在一点M,使得△DCM∽△BQC?如果存在,求出点M的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
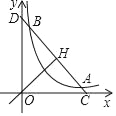
【题目】如图,已知直线y=﹣x+b(b>0)与其垂线y=x交于H,与双曲线c:y=![]() (k>0)在第一象限交于A,B,与两坐标轴交于C,D.
(k>0)在第一象限交于A,B,与两坐标轴交于C,D.
(1)当A的坐标为(2,1)时,求k的值和OH的长;
(2)若CH2﹣HA2=4,求双曲线c的方程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某日的钱塘江观潮信息如图:

按上述信息,小红将“交叉潮”形成后潮头与乙地之间的距离s(千米)与时间t(分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点A(0,12),点B坐标为(m,0),曲线BC可用二次函数s=![]() t2+bt+c(b,c是常数)刻画.
t2+bt+c(b,c是常数)刻画.
(1)求m的值,并求出潮头从甲地到乙地的速度;
(2)11:59时,小红骑单车从乙地出发,沿江边公路以0.48千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为0.48千米/分,小红逐渐落后.问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度v=v0+![]() (t﹣30),v0是加速前的速度).
(t﹣30),v0是加速前的速度).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店准备购进甲、乙两种服装出售,甲种每件售价120元,乙种每件售价90元.每件甲服装的进价比乙服装的进价贵20元,购进3件甲服装的费用和购进4件乙服装的费用相等,现计划购进两种服装共100件,其中甲种服装不少于65件.
(1)甲种服装进价为 元/件,乙种服装进价为 元/件;
(2)若购进这100件服装的费用不得超过7500元.
①求甲种服装最多购进多少件?
②该服装店对甲种服装每件降价![]() 元,乙种服装价格不变,如果这100件服装都可售完,那么该服装店如何进货才能获得最大利润?
元,乙种服装价格不变,如果这100件服装都可售完,那么该服装店如何进货才能获得最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,∠BAD=60°,AC=AD,AC平分∠BAD,M,N分别为AC,CD的中点,BM的延长线交AD于点E,连接MN,BN.对于下列四个结论:①MN∥AD;② BM=MN;③△BAE≌△ACB;④AD=![]() BN,其中正确结论的序号是( )
BN,其中正确结论的序号是( )

A. ①②③④ B. ①②③ C. ①②④ D. ①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分图象如图所示,图象过点
的部分图象如图所示,图象过点![]() ,对称轴为直线
,对称轴为直线![]() ,下列结论:
,下列结论: ![]() ;
; ![]() ;
; ![]() ;
; ![]() 若点
若点![]() 、点
、点![]() 、点
、点![]() 在该函数图象上,则
在该函数图象上,则![]() ;
; ![]() 若方程
若方程![]() 的两根为
的两根为![]() 和
和![]() ,且
,且![]() ,则
,则![]() 其中正确的结论是______.
其中正确的结论是______.
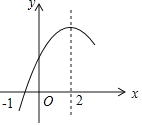
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 都在数轴上,
都在数轴上,![]() 为原点.
为原点.
(1)点![]() 表示的数是 ;
表示的数是 ;
(2)若点![]() 以每秒3个单位长度的速度沿数轴运动,则1秒后点
以每秒3个单位长度的速度沿数轴运动,则1秒后点![]() 表示的数是 ;
表示的数是 ;
(3)若点![]() 都以每秒3个单位长度的速度沿数轴向右运动,而点
都以每秒3个单位长度的速度沿数轴向右运动,而点![]() 不动,
不动,![]() 秒后有一个点是一条线段的中点,求
秒后有一个点是一条线段的中点,求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com