
【题目】如图,在四边形ABCD中,∠ABC=90°,∠BAD=60°,AC=AD,AC平分∠BAD,M,N分别为AC,CD的中点,BM的延长线交AD于点E,连接MN,BN.对于下列四个结论:①MN∥AD;② BM=MN;③△BAE≌△ACB;④AD=![]() BN,其中正确结论的序号是( )
BN,其中正确结论的序号是( )

A. ①②③④ B. ①②③ C. ①②④ D. ①②
【答案】C
【解析】分析: 根据三角形中位线定理,直角三角形斜边上的中线一一判断即可.
详解:①在△CAD中,∵M、N分别是AC、CD的中点,∴MN∥AD,正确.
②在△CAD中,∵M、N分别是AC、CD的中点,∴MN∥AD,MN=![]() AD,
AD,
在RT△ABC中,∵M是AC中点,∴BM=![]() AC,∵AC=AD,∴BM=MN.正确.
AC,∵AC=AD,∴BM=MN.正确.
③错误.
④设AM=x,∵∠BAD=60°,AC平分∠BAD,∴∠BAC=∠DAC=30°,∵∠ABC=90°,M为AC的中点,∴BM=AM=x,∴∠CMB=2∠BAC=60°,∵AC=AD,∴AD=2x,∵M,N分别为AC,CD的中点,∴MN=![]() AD=x,∠CMN=∠DAC=30°,∴∠BMN=90°,∴BN=
AD=x,∠CMN=∠DAC=30°,∴∠BMN=90°,∴BN=![]() ,∴
,∴![]() BN=AD.故正确.
BN=AD.故正确.
故答案为:C.


科目:初中数学 来源: 题型:
【题目】唐山质量监督局从某食品厂生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,把超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值(单位:克) | ﹣6 | ﹣2 | 0 | 1 | 3 | 4 |
袋数 | 1 | 4 | 3 | 4 | 5 | 3 |
(1)若每袋食品的标准质量为450克,则抽样检测的20袋食品的总质量是多少克?
(2)若该种食品的合格标准为450±5克,求该种食品抽样检测的合格率?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是小明在健身器材上进行仰卧起坐锻炼时的情景,图②是小明锻炼时上半身由ON位置运动到与地面垂直的OM位置时的示意图.已知AC=0.66米,BD=0.26米,α=20°.(参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364)

(1)求AB的长(精确到0.01米);
(2)若测得ON=0.8米,试计算小明头顶由N点运动到M点的路径![]() 的长度.(结果保留π)
的长度.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用24000元购入一批空调,然后以每台3000元的价格销售,因天气炎热,空调很快售完;商场又以52000元的价格再次购入该种型号的空调,数量是第一次购入的2倍,但购入的单价上调了200元,售价每台也上调了200元.
(1)商场第一次购入的空调每台进价是多少元?
(2)商场既要尽快售完第二次购入的空调,又要在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售,最多可将多少台空调打折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若将一根绳子平放在桌上,用剪刀任意剪n刀(如图①),绳子变成n+1段;若将绳子对折1次后从中间剪一刀(如图②),绳子的刀口 个,绳子变成 段;若将绳子对折2次后从中间剪一刀,绳子的刀口有 个,绳子变成 段;若将绳子对折n次后从中间剪一刀,绳子的刀口 个,绳子变成 段.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在数轴上表示的数分别为-4和+16,A,B两点间的距离可记为AB
![]()
(1) 点C在数轴上A,B两点之间,且AC=BC,则C点对应的数是_________
(2) 点C在数轴上A,B两点之间,且BC=4AC,则C点对应的数是_________
(3) 点C在数轴上,且AC+BC=30,求点C对应的数?
(4) 若点A在数轴上表示的数是a,B表示的数是b,则AB=_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是边长为![]() 的正方形ABCD的对角线BD上的动点,过点P分别作PE⊥BC于点E,PF⊥DC于点F,连接AP并延长,交射线BC于点H,交射线DC于点M,连接EF交AH于点G,当点P在BD上运动时(不包括B、D两点),以下结论中:①MF=MC;②AH⊥EF;③AP2=PMPH;④EF的最小值是
的正方形ABCD的对角线BD上的动点,过点P分别作PE⊥BC于点E,PF⊥DC于点F,连接AP并延长,交射线BC于点H,交射线DC于点M,连接EF交AH于点G,当点P在BD上运动时(不包括B、D两点),以下结论中:①MF=MC;②AH⊥EF;③AP2=PMPH;④EF的最小值是![]() .其中正确结论是( )
.其中正确结论是( )

A. ①③ B. ②③ C. ②③④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
如果一个三角形的三边长分别为a,b,c,记p=![]() ,那么这个三角形的面积S=
,那么这个三角形的面积S=![]() .这个公式叫“海伦公式”,它是利用三角形三条边的边长直接求三角形面积的公式。中国的秦九韶也得出了类似的公式,称三斜求积术,故这个公式又被称为“海伦秦---九韶公式”完成下列问题:
.这个公式叫“海伦公式”,它是利用三角形三条边的边长直接求三角形面积的公式。中国的秦九韶也得出了类似的公式,称三斜求积术,故这个公式又被称为“海伦秦---九韶公式”完成下列问题:
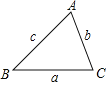
如图,在△ABC中,a=7,b=5,c=6.
(1)求△ABC的面积;
(2)设AB边上的高为h1,AC边上的高为h2,求h1 +h2的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com