
【题目】用因式分解法解下列方程;
①(x+2)2﹣9=0
②(2x﹣3)2=3(2x﹣3)
③x2﹣6x+9=0
④(x+5)(x﹣1)=7.
【答案】①x1=﹣5,x2=1;②x1=![]() ,x2=3;③x1=x2=3;④x1=﹣6,x2=2.
,x2=3;③x1=x2=3;④x1=﹣6,x2=2.
【解析】
①由整体思想用平方差公式分解就可以求出结论;
②先移项,再提公因式就可以求出结论;
③直接由完全平方公式求解即可
④先展开,再移项,转化为一般形式后由十字相乘法分解因式即可.
:①分解因式,得
(x+2+3)(x+2﹣3)=0,
∴x+5=0或x﹣1=0
∴x1=﹣5,x2=1;
②移项,得
(2x﹣3)2﹣3(2x﹣3)=0
提公因式,得
(2x﹣3)(2x﹣3﹣3)=0,
∴2x﹣3=0或2x﹣6=0
∴x1=![]() ,x2=3;
,x2=3;
③由完全平方公式分解因式,得
(x﹣3)2=0,
∴x﹣3=0
∴x1=x2=3
(4)变形为:
x2+4x﹣5=7,
移项,得
x2+4x﹣5﹣7=0,
x2+4x﹣12=0
∴(x+6)(x﹣2)=0,
∴x+6=0或x﹣2=0
∴x1=﹣6,x2=2.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
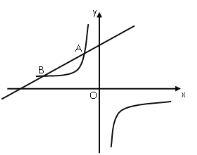
【题目】如图,一次函数![]() (
(![]() 为常数,且
为常数,且![]() )的图像与反比例函数
)的图像与反比例函数![]() 的图像交于
的图像交于![]() ,
,![]() 两点.
两点.
(1)求一次函数的表达式;
(2)若将直线![]() 向下平移
向下平移![]() 个单位长度后与反比例函数的图像有且只有一个公共点,求
个单位长度后与反比例函数的图像有且只有一个公共点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校要从小明和小亮两名运动员中挑出一人参加立定跳远比赛,学校记录了二人在最近的6次立定跳远选拔赛中的成绩(单位:cm),并进行整理、描述和分析.下面给出了部分信息.
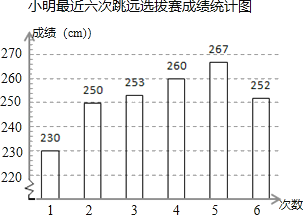
a.如图
b.小亮最近6次选拔赛成绩如下:
250 | 254 | 260 | 271 | 255 | 240 |
c.小明和小亮最近6次选拔赛中成绩的平均数、中位数、方差如下:
平均数 | 中位数 | 方差 | |
小明 | 252 | 252.5 | 129.7 |
小亮 | 255 | m | 88.7 |
根据以上信息,回答下列问题:
(1)m= ;
(2)历届比赛表明:成绩达到266cm就有可能夺冠,成绩达到270cm就能打破纪录(积分加倍),根据这6次选拔赛成绩,你认为应选 (填“小明”或“小亮”)参加这项比赛,理由是 .(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
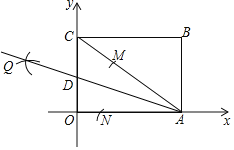
【题目】如图,四边形OABC为矩形,点A,C分别在x轴和y轴上,连接AC,点B的坐标为(8,6),以A为圆心,任意长为半径画弧,分别交AC、AO于点M、N,再分别以M、N为圆心,大于![]() MN长为半径画弧两弧交于点Q,作射线AQ交y轴于点D,则点D的坐标为( )
MN长为半径画弧两弧交于点Q,作射线AQ交y轴于点D,则点D的坐标为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某户外看台的截面图,长10m的看台AB与水平地面AP的夹角为35°,与AP平行的平台BC长为1.9m,点F是遮阳棚DE上端E正下方在地面上的一点,测得AF=2m,在挡风墙CD的点D处测得点E的仰角为26°,求遮阳棚DE的长. (参考数据:sin35°≈0.57,cos35°≈0.82, sin26°≈0.44,cos26°≈0.90)
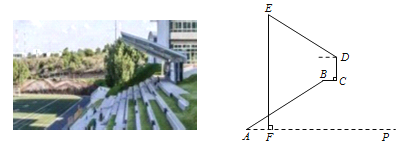
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程(m-1)x2+(m+1)x+3m-1=0,当m_________时,是一元一次方程;当m_________时,是一元二次方程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目).并将调查结果绘制成如下统计图表:
学生最喜欢的节目人数统计表
节目 | 人数(名) | 百分比 |
最强大脑 | 5 | 10% |
阅读者 | 15 | B% |
中国诗词大会 | a | 40% |
出彩中国人 | 10 | 20% |
根据以上提供的信息,解答下列问题
(1)x= ,a= ,b= ;
(2)补全条形统计图;
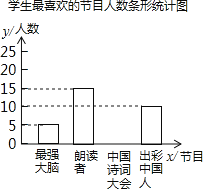
(3)若该校共有学生800名,根据抽样调查结果,估计该校喜爱《中国诗词大会》节目的学生有多少名?
(4)李玲和王亮经过选拔代表班级参加校内即将举办的“中国诗词大会”,预赛分为A、B、C三组进行,由抽签确定分组.李玲和王亮恰好分在一组的概率是多少?(要求用画树状图或列表法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴相交于
与x轴相交于![]() 两点,(点A在B点左侧)与y轴交于点C.
两点,(点A在B点左侧)与y轴交于点C.
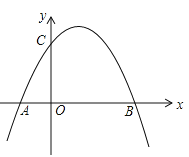
(Ⅰ)求![]() 两点坐标.
两点坐标.
(Ⅱ)连结![]() ,若点P在第一象限的抛物线上,P的横坐标为t,四边形
,若点P在第一象限的抛物线上,P的横坐标为t,四边形![]() 的面积为S.试用含t的式子表示S,并求t为何值时,S最大.
的面积为S.试用含t的式子表示S,并求t为何值时,S最大.
(Ⅲ)在(Ⅱ)的基础上,若点![]() 分别为抛物线及其对称轴上的点,点G的横坐标为m,点H的纵坐标为n,且使得以
分别为抛物线及其对称轴上的点,点G的横坐标为m,点H的纵坐标为n,且使得以![]() 四点构成的四边形为平行四边形,求满足条件的
四点构成的四边形为平行四边形,求满足条件的![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com