
【题目】如图,抛物线![]() 与x轴相交于
与x轴相交于![]() 两点,(点A在B点左侧)与y轴交于点C.
两点,(点A在B点左侧)与y轴交于点C.
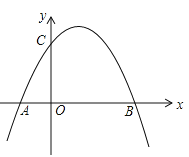
(Ⅰ)求![]() 两点坐标.
两点坐标.
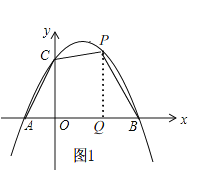
(Ⅱ)连结![]() ,若点P在第一象限的抛物线上,P的横坐标为t,四边形
,若点P在第一象限的抛物线上,P的横坐标为t,四边形![]() 的面积为S.试用含t的式子表示S,并求t为何值时,S最大.
的面积为S.试用含t的式子表示S,并求t为何值时,S最大.
(Ⅲ)在(Ⅱ)的基础上,若点![]() 分别为抛物线及其对称轴上的点,点G的横坐标为m,点H的纵坐标为n,且使得以
分别为抛物线及其对称轴上的点,点G的横坐标为m,点H的纵坐标为n,且使得以![]() 四点构成的四边形为平行四边形,求满足条件的
四点构成的四边形为平行四边形,求满足条件的![]() 的值.
的值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ,当
,当![]() 时,
时,![]() ;(Ⅲ)满足条件的点
;(Ⅲ)满足条件的点![]() 的值为:
的值为:![]() ,或
,或![]() ,或
,或![]()
【解析】
(Ⅰ)令y=0,建立方程求解即可得出结论;
(Ⅱ)设出点P的坐标,利用S=S△AOC+S梯形OCPQ+S△PQB,即可得出结论;
(Ⅲ)分三种情况,利用平行四边形的性质对角线互相平分和中点坐标公式建立方程组即可得出结论.
解:(Ⅰ)抛物线![]() ,
,
令![]() ,则
,则![]() ,
,
解得:![]() 或
或![]() ,
,
∴![]()
(Ⅱ)由抛物线![]() ,令
,令![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
如图1,点P作![]() 轴于Q,
轴于Q,
∵P的横坐标为t,∴设![]() ,
,
∴![]()
∴![]()
![]()
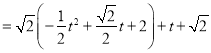
![]() ,
,
∴当![]() 时,
时,![]() ;
;
(Ⅲ)由(Ⅱ)知,![]() ,
,
∴![]() ,
,
∵抛物线![]() 的对称轴为
的对称轴为![]() ,
,
∴设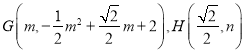
以![]() 四点构成的四边形为平行四边形,
四点构成的四边形为平行四边形,![]() ,
,
①当![]() 和
和![]() 为对角线时,
为对角线时,
∴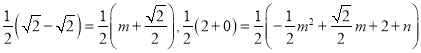 ,
,
∴![]() ,
,
②当![]() 和
和![]() 是对角线时,
是对角线时,
∴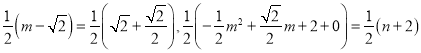 ,
,
∴![]() ,
,
③![]() 和
和![]() 为对角线时,
为对角线时,
∴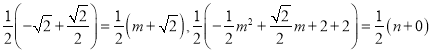 ,
,
∴![]() ,
,
即:满足条件的点![]() 的值为:
的值为:
![]() ,或
,或![]() ,或
,或![]()


 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】解不等式组 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得_______________;
(Ⅱ)解不等式②,得_______________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:

(Ⅳ)原不等式组的解集为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组: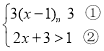 请结合题意填空,完成本题的解答:
请结合题意填空,完成本题的解答:
(Ⅰ)解不等式①,得:_________________;
(Ⅱ)解不等式②,得:_________________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来;

(IV)原不等式组的解集为:_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
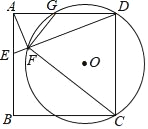
【题目】如图,在正方形ABCD中,E是AB上一点,连接DE.过点A作AF⊥DE,垂足为F,⊙O经过点C、D、F,与AD相交于点G.
(1)求证:△AFG∽△DFC;
(2)若正方形ABCD的边长为4,AE=1,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
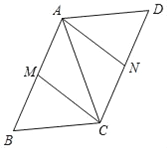
【题目】已知:如图,平行四边形ABCD中,M、N分别为AB和CD的中点.
(1)求证:四边形AMCN是平行四边形;
(2)若AC=BC=5,AB=6,求四边形AMCM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,则下列结论:
①2a+b+c>0;②a﹣b+c<0;③x(ax+b)≤a+b;④a<﹣1.
其中正确的有( )
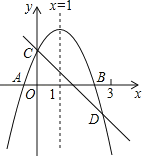
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
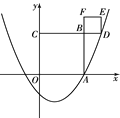
【题目】如图,抛物线![]() 与
与![]() 轴正半轴交于点A(3,0).以OA为边在
轴正半轴交于点A(3,0).以OA为边在![]() 轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF,则
轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF,则![]() = ,点E的坐标是 .
= ,点E的坐标是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com