
【题目】解不等式组: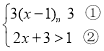 请结合题意填空,完成本题的解答:
请结合题意填空,完成本题的解答:
(Ⅰ)解不等式①,得:_________________;
(Ⅱ)解不等式②,得:_________________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来;

(IV)原不等式组的解集为:_________________.
科目:初中数学 来源: 题型:
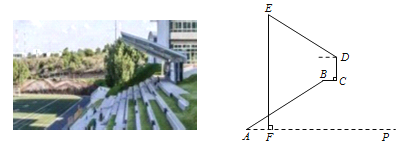
【题目】如图是某户外看台的截面图,长10m的看台AB与水平地面AP的夹角为35°,与AP平行的平台BC长为1.9m,点F是遮阳棚DE上端E正下方在地面上的一点,测得AF=2m,在挡风墙CD的点D处测得点E的仰角为26°,求遮阳棚DE的长. (参考数据:sin35°≈0.57,cos35°≈0.82, sin26°≈0.44,cos26°≈0.90)
查看答案和解析>>
科目:初中数学 来源: 题型:
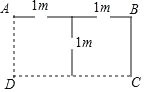
【题目】如图,利用两面靠墙(墙足够长),用总长度37米的篱笆(图中实线部分)围成一个矩形鸡舍ABCD,且中间共留三个1米的小门,设篱笆BC长为x米.
(1)AB=______.(用含x的代数式表示)
(2)若矩形鸡舍ABCD 面积为150平方米,求篱笆BC的长.
(3)矩形鸡舍ABCD面积是否有可能达到210平方米?若有可能,求出相应x的值;若不可能,则说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民用水实行以户为单位的三级阶梯收费办法:
第一级:居民每户每月用水![]() 吨以内含
吨以内含![]() 吨,每吨收水费
吨,每吨收水费![]() 元;
元;
第二级:居民每户每月用水超过![]() 吨但不超过
吨但不超过![]() 吨,未超过
吨,未超过![]() 的部分按照第一级标准收费,超过部分每吨收水费
的部分按照第一级标准收费,超过部分每吨收水费![]() 元;
元;
第三级:居民每户每月用水超过![]() 吨,未超过
吨,未超过![]() 吨的部分按照第一、二级标准收费,超过部分每吨收水费
吨的部分按照第一、二级标准收费,超过部分每吨收水费![]() 元;
元;
设一户居民月用水![]() 吨,应缴水费
吨,应缴水费![]() 元,
元,![]() 与
与![]() 之间的函数关系如图所示,
之间的函数关系如图所示,
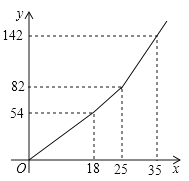
(Ⅰ)根据图象直接作答:![]() ___________,
___________,![]() _______________,
_______________,![]() _______________;
_______________;
(Ⅱ)求当![]() 时,
时,![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(Ⅲ)把上述水费阶梯收费办法称为方案①,假设还存在方案②;居民每户月用水一律按照每吨![]() 元的标准缴费.当居民用户月用水超过
元的标准缴费.当居民用户月用水超过![]() 吨时,请你根据居民每户月用水量的大小设计出对居民缴费最实惠的方案.
吨时,请你根据居民每户月用水量的大小设计出对居民缴费最实惠的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴相交于
与x轴相交于![]() 两点,(点A在B点左侧)与y轴交于点C.
两点,(点A在B点左侧)与y轴交于点C.
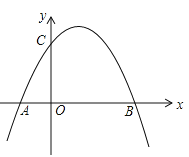
(Ⅰ)求![]() 两点坐标.
两点坐标.
(Ⅱ)连结![]() ,若点P在第一象限的抛物线上,P的横坐标为t,四边形
,若点P在第一象限的抛物线上,P的横坐标为t,四边形![]() 的面积为S.试用含t的式子表示S,并求t为何值时,S最大.
的面积为S.试用含t的式子表示S,并求t为何值时,S最大.
(Ⅲ)在(Ⅱ)的基础上,若点![]() 分别为抛物线及其对称轴上的点,点G的横坐标为m,点H的纵坐标为n,且使得以
分别为抛物线及其对称轴上的点,点G的横坐标为m,点H的纵坐标为n,且使得以![]() 四点构成的四边形为平行四边形,求满足条件的
四点构成的四边形为平行四边形,求满足条件的![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列选项中,是反比例函数关系的为
A. 在直角三角形中,30°角所对的直角边y与斜边x之间的关系
B. 在等腰三角形中,顶角y与底角x之间的关系
C. 圆的面积S与它的直径d之间的关系
D. 面积为20的菱形,其中一条对角线y与另一条对角线x之间的关系
查看答案和解析>>
科目:初中数学 来源: 题型:
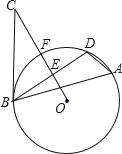
【题目】如图,△ABD是⊙O的内接三角形,E是弦BD的中点,点C是⊙O外一点且∠DBC=∠A,连接OE延长与圆相交于点F,与BC相交于点C.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为6,BC=8,求弦BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“数学迷”小楠通过从“特殊到一般”的过程,对倍角三角形(一个内角是另一个内角的2倍的三角形)进行研究,得出结论:如图1,在![]() 中,
中,![]() 、
、![]() 、
、![]() 的对边分别是
的对边分别是![]() 、
、![]() 、
、![]() ,如果
,如果![]() ,那么
,那么![]() .下面给出小楠对其中一种特殊情形的一种证明方法.
.下面给出小楠对其中一种特殊情形的一种证明方法.
已知:如图2,在△![]() 中,
中,![]() ,
,![]() .求证:
.求证:![]() .
.
证明:如图2,延长![]() 到
到![]() ,使得
,使得![]() .
.
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
又![]() ,
,
∴△![]() △
△![]() .
.
∴![]() ,即
,即![]() .
.
∴![]() .
.
根据上述材料提供的信息,请你完成下列情形的证明(用不同于材料中的方法也可以);
已知:如图1,在△![]() 中,
中,![]() .
.
求证:![]() .
.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com