
ЁОЬтФПЁПЁАЪ§бЇУдЁБаЁщЊЭЈЙ§ДгЁАЬиЪтЕНвЛАуЁБЕФЙ§ГЬЃЌЖдБЖНЧШ§НЧаЮЃЈвЛИіФкНЧЪЧСэвЛИіФкНЧЕФ2БЖЕФШ§НЧаЮЃЉНјаабаОПЃЌЕУГіНсТлЃКШчЭМ1,дк![]() жаЃЌ
жаЃЌ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЕФЖдБпЗжБ№ЪЧ
ЕФЖдБпЗжБ№ЪЧ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌШчЙћ
ЃЌШчЙћ![]() ЃЌФЧУД
ЃЌФЧУД![]() ЃЎЯТУцИјГіаЁщЊЖдЦфжавЛжжЬиЪтЧщаЮЕФвЛжжжЄУїЗНЗЈЃЎ
ЃЎЯТУцИјГіаЁщЊЖдЦфжавЛжжЬиЪтЧщаЮЕФвЛжжжЄУїЗНЗЈЃЎ
вбжЊЃКШчЭМ2ЃЌдкЁї![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЎЧѓжЄЃК
ЃЎЧѓжЄЃК![]() ЃЎ
ЃЎ
жЄУїЃКШчЭМ2ЃЌбгГЄ![]() ЕН
ЕН![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЎ
ЃЎ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ
гж![]() ЃЌ
ЃЌ
ЁрЁї![]() Ёї
Ёї![]() ЃЎ
ЃЎ
Ёр![]() ЃЌМД
ЃЌМД![]() ЃЎ
ЃЎ
Ёр![]() ЃЎ
ЃЎ
ИљОнЩЯЪіВФСЯЬсЙЉЕФаХЯЂЃЌЧыФуЭъГЩЯТСаЧщаЮЕФжЄУїЃЈгУВЛЭЌгкВФСЯжаЕФЗНЗЈвВПЩвдЃЉЃЛ
вбжЊЃКШчЭМ1ЃЌдкЁї![]() жаЃЌ
жаЃЌ![]() ЃЎ
ЃЎ
ЧѓжЄЃК![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНтВЛЕШЪНзщЃК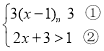 ЧыНсКЯЬтвтЬюПеЃЌЭъГЩБОЬтЕФНтД№ЃК
ЧыНсКЯЬтвтЬюПеЃЌЭъГЩБОЬтЕФНтД№ЃК
ЃЈЂёЃЉНтВЛЕШЪНЂйЃЌЕУЃК_________________ЃЛ
ЃЈЂђЃЉНтВЛЕШЪНЂкЃЌЕУЃК_________________ЃЛ
ЃЈЂѓЃЉАбВЛЕШЪНЂйКЭЂкЕФНтМЏдкЪ§жсЩЯБэЪОГіРДЃЛ

ЃЈIVЃЉдВЛЕШЪНзщЕФНтМЏЮЊЃК_________________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕ![]() жагаОиаЮ
жагаОиаЮ![]() ЃЌ
ЃЌ![]() ЃЌНЋОиаЮ
ЃЌНЋОиаЮ![]() ШЦдЕу
ШЦдЕу![]() ФцЪБеыа§зЊЕУЕНОиаЮOAЁфBЁфCЁф.
ФцЪБеыа§зЊЕУЕНОиаЮOAЁфBЁфCЁф.
(Ђё)ШчЭМ1ЃЌЕБЕуAЁфЪзДЮТфдк![]() ЩЯЪБЃЌЧѓа§зЊНЧЃЛ
ЩЯЪБЃЌЧѓа§зЊНЧЃЛ
(Ђђ)дк(Ђё)ЕФЬѕМўЯТЧѓЕуBЁфЕФзјБъЃЛ
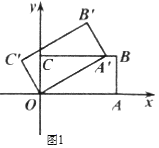
(Ђѓ)ШчЭМ2ЃЌЕБЕуBЁфЪзДЮТфдк![]() жсЩЯЪБЃЌжБНгаДГіДЫЪБЕуAЁфЕФзјБъ.
жсЩЯЪБЃЌжБНгаДГіДЫЪБЕуAЁфЕФзјБъ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§yЃНЉx2Љ2x+3ЃЎ
ЃЈ1ЃЉАбКЏЪ§ЙиЯЕЪНХфГЩЖЅЕуЪНВЂЧѓГіЭМЯѓЕФЖЅЕузјБъКЭЖдГЦжсЃЎ
ЃЈ2ЃЉШєЭМЯѓгыxжсНЛЕуЮЊAЃЎBЃЌгыyжсНЛЕуЮЊCЃЌЧѓAЁЂBЁЂCШ§ЕуЕФзјБъЃЛ
ЃЈ3ЃЉдкЭМжаЛГіЭМЯѓЃЎВЂЧѓГіЁїABCУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЈ1ЃЉЃЌвбжЊЁЯ![]() ,Еу
,Еу![]() ЮЊЩфЯп
ЮЊЩфЯп![]() ЩЯвЛЕуЃЌЧв
ЩЯвЛЕуЃЌЧв![]() ЃЌ
ЃЌ![]() ЁЂ
ЁЂ![]() ЮЊЩфЯп
ЮЊЩфЯп![]() КЭ
КЭ![]() ЩЯЕФСНИіЖЏЕуЃЈ
ЩЯЕФСНИіЖЏЕуЃЈ![]() ЃЉЃЌЙ§Еу
ЃЉЃЌЙ§Еу![]() зї
зї![]() ЁЭ
ЁЭ![]() ЃЌДЙзуЮЊЕу
ЃЌДЙзуЮЊЕу![]() ЃЌЧв
ЃЌЧв![]() ЃЌСЊНс
ЃЌСЊНс![]() ЃЎ
ЃЎ
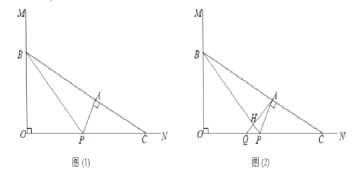
ЃЈ1ЃЉШє![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЩш![]() ЃЌ
ЃЌ![]() Чѓ
Чѓ![]() гы
гы![]() жЎМфЕФКЏЪ§НтЮіЪНЃЌВЂаДГіЖЈвхгђЃЛ
жЎМфЕФКЏЪ§НтЮіЪНЃЌВЂаДГіЖЈвхгђЃЛ
ЃЈ3ЃЉШчЭМ(2)ЃЌЙ§Еу![]() зї
зї![]() ЕФДЙЯпЃЌДЙзуЮЊЕу
ЕФДЙЯпЃЌДЙзуЮЊЕу![]() ЃЌНЛЩфЯп
ЃЌНЛЩфЯп![]() гкЕу
гкЕу![]() ЃЌЕу
ЃЌЕу![]() ЁЂ
ЁЂ![]() дкЩфЯп
дкЩфЯп![]() КЭ
КЭ![]() ЩЯдЫЖЏЪБЃЌЬНЫїЯпЖЮ
ЩЯдЫЖЏЪБЃЌЬНЫїЯпЖЮ![]() ЕФГЄЪЧЗёЗЂЩњБфЛЏЃПШєВЛЗЂЩњБфЛЏЃЌЧѓГіЫќЕФжЕЁЃШєЗЂЩњБфЛЏЃЌЪдгУКЌxЕФДњЪ§ЪНБэЪО
ЕФГЄЪЧЗёЗЂЩњБфЛЏЃПШєВЛЗЂЩњБфЛЏЃЌЧѓГіЫќЕФжЕЁЃШєЗЂЩњБфЛЏЃЌЪдгУКЌxЕФДњЪ§ЪНБэЪО![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
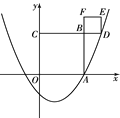
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() гы
гы![]() жсе§АыжсНЛгкЕуAЃЈ3ЃЌ0ЃЉЃЎвдOAЮЊБпдк
жсе§АыжсНЛгкЕуAЃЈ3ЃЌ0ЃЉЃЎвдOAЮЊБпдк![]() жсЩЯЗНзїе§ЗНаЮOABCЃЌбгГЄCBНЛХзЮяЯпгкЕуDЃЌдйвдBDЮЊБпЯђЩЯзїе§ЗНаЮBDEFЃЌдђ
жсЩЯЗНзїе§ЗНаЮOABCЃЌбгГЄCBНЛХзЮяЯпгкЕуDЃЌдйвдBDЮЊБпЯђЩЯзїе§ЗНаЮBDEFЃЌдђ![]() = ЃЌЕуEЕФзјБъЪЧ ЃЎ
= ЃЌЕуEЕФзјБъЪЧ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЯТСаВФСЯЃЌЭъГЩШЮЮёЃК
здЯрЫЦЭМаЮ
ЖЈвхЃКШєФГИіЭМаЮПЩЗжИюЮЊШєИЩИіЖМгыЫќЯрЫЦЕФЭМаЮЃЌдђГЦетИіЭМаЮЪЧздЯрЫЦЭМаЮ.Р§ШчЃК
е§ЗНаЮ![]() жаЃЌЕу
жаЃЌЕу![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() БпЕФжаЕуЃЌСЌНг
БпЕФжаЕуЃЌСЌНг![]() ЃЌ
ЃЌ![]() НЛгкЕу
НЛгкЕу![]() ЃЌвзжЊЗжИюГЩЕФЫФИіЫФБпаЮ
ЃЌвзжЊЗжИюГЩЕФЫФИіЫФБпаЮ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ОљЮЊе§ЗНаЮЃЌЧвгыде§ЗНаЮЯрЫЦЃЌЙЪе§ЗНаЮЪЧздЯрЫЦЭМаЮ.
ОљЮЊе§ЗНаЮЃЌЧвгыде§ЗНаЮЯрЫЦЃЌЙЪе§ЗНаЮЪЧздЯрЫЦЭМаЮ.
ШЮЮёЃК
ЃЈ1ЃЉЭМ1жае§ЗНаЮ![]() ЗжИюГЩЕФЫФИіаЁе§ЗНаЮжаЃЌУПИіе§ЗНаЮгыде§ЗНаЮЕФЯрЫЦБШЮЊ_______ЃЛ
ЗжИюГЩЕФЫФИіаЁе§ЗНаЮжаЃЌУПИіе§ЗНаЮгыде§ЗНаЮЕФЯрЫЦБШЮЊ_______ЃЛ
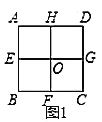
ЃЈ2ЃЉШчЭМ2ЃЌвбжЊ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌаЁУїЗЂЯж
ЃЌаЁУїЗЂЯж![]() вВЪЧЁАздЯрЫЦЭМаЮЁБЃЌЫћЕФЫМТЗЪЧЃКЙ§Еу
вВЪЧЁАздЯрЫЦЭМаЮЁБЃЌЫћЕФЫМТЗЪЧЃКЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌдђ
ЃЌдђ![]() НЋ
НЋ![]() ЗжИюГЩ2ИігыЫќздМКЯрЫЦЕФаЁжБНЧШ§НЧаЮ.дђ
ЗжИюГЩ2ИігыЫќздМКЯрЫЦЕФаЁжБНЧШ§НЧаЮ.дђ![]() гы
гы![]() ЕФЯрЫЦБШЮЊ________ЃЛдђ
ЕФЯрЫЦБШЮЊ________ЃЛдђ![]() гы
гы![]() ЕФЯрЫЦБШЮЊ_______;
ЕФЯрЫЦБШЮЊ_______;
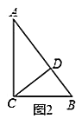
ЃЈ3ЃЉЯжгавЛИіОиаЮ![]() ЪЧздЯрЫЦЭМаЮЃЌЦфжаГЄ
ЪЧздЯрЫЦЭМаЮЃЌЦфжаГЄ![]() ЃЌПэ
ЃЌПэ![]() .
.
ЂйШчЭМ3-1ЃЌШєНЋОиаЮ![]() знЯђЗжИюГЩСНИіШЋЕШОиаЮЃЌЧвгыдОиаЮЖМЯрЫЦЃЌдђ
знЯђЗжИюГЩСНИіШЋЕШОиаЮЃЌЧвгыдОиаЮЖМЯрЫЦЃЌдђ![]() _____ЃЈгУКЌ
_____ЃЈгУКЌ![]() ЕФЪНзгБэЪОЃЉЃЛ
ЕФЪНзгБэЪОЃЉЃЛ
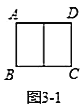
ЂкШчЭМ3-2ШєНЋОиаЮ![]() знЯђЗжИюГЩ
знЯђЗжИюГЩ![]() ИіШЋЕШОиаЮЃЌЧвгыдОиаЮЖМЯрЫЦЃЌдђ
ИіШЋЕШОиаЮЃЌЧвгыдОиаЮЖМЯрЫЦЃЌдђ![]() ______ЃЈгУКЌ
______ЃЈгУКЌ![]() ЃЌ
ЃЌ![]() ЕФЪНзгБэЪОЃЉЃЛ
ЕФЪНзгБэЪОЃЉЃЛ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁППЮЬУЩЯЃЌРЯЪІИјГівЛЕРЬтЃКШчЭМЃЌНЋХзЮяЯпCЃКyЃНx2Љ6x+5дкxжсЯТЗНЕФЭМЯѓбиxжсЗелЃЌЗелКѓЕУЕНЕФЭМЯѓгыХзЮяЯпCдкxжсЩЯЗНЕФЭМЯѓМЧЮЊGЃЌвбжЊжБЯпlЃКyЃНx+mгыЭМЯѓGгаСНИіЙЋЙВЕуЃЌЧѓmЕФШЁжЕЗЖЮЇМзЭЌбЇЕФНсЙћЪЧЉ5ЃМmЃМЉ1ЃЌввЭЌбЇЕФНсЙћЪЧmЃО![]() ЃЎЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
ЃЎЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
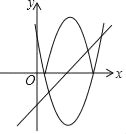
A.МзЕФНсЙће§ШЗ
B.ввЕФНсЙће§ШЗ
C.МзЁЂввЕФНсЙћКЯдквЛЦ№ВХе§ШЗ
D.МзЁЂввЕФНсЙћКЯдквЛЦ№вВВЛе§ШЗ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЯпЖЮABЁЂCDЗжБ№БэЪОМзввСННЈжўЮяЕФИпЃЌBAЁЭADЃЌCDЁЭDAЃЌДЙзуЗжБ№ЮЊAЁЂDЃЎДгDЕуВтЕНBЕуЕФбіНЧІСЮЊ60ЁуЃЌДгCЕуВтЕУBЕуЕФбіНЧІТЮЊ30ЁуЃЌМзНЈжўЮяЕФИпAB=30Уз
ЃЈ1ЃЉЧѓМзЁЂввСННЈжўЮяжЎМфЕФОрРыADЃЎ
ЃЈ2ЃЉЧѓввНЈжўЮяЕФИпCDЃЎ
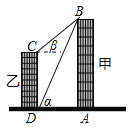
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com