
【题目】如图,在平面直角坐标系![]() 中有矩形
中有矩形![]() ,
,![]() ,将矩形
,将矩形![]() 绕原点
绕原点![]() 逆时针旋转得到矩形OA′B′C′.
逆时针旋转得到矩形OA′B′C′.
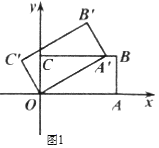
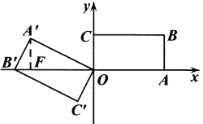
(Ⅰ)如图1,当点A′首次落在![]() 上时,求旋转角;
上时,求旋转角;
(Ⅱ)在(Ⅰ)的条件下求点B′的坐标;
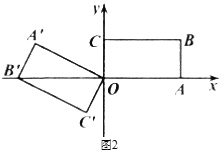
(Ⅲ)如图2,当点B′首次落在![]() 轴上时,直接写出此时点A′的坐标.
轴上时,直接写出此时点A′的坐标.
【答案】(Ⅰ)旋转角为![]() ;(Ⅱ)B′的坐标为
;(Ⅱ)B′的坐标为![]() ;(Ⅲ)点A′的坐标为
;(Ⅲ)点A′的坐标为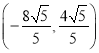
【解析】
(Ⅰ)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,由旋转的性质及A、C坐标可得OA=OA′=4,A′D=A′B′=OC=2,由A′D=
,由旋转的性质及A、C坐标可得OA=OA′=4,A′D=A′B′=OC=2,由A′D=![]() OA′可得
OA′可得![]() ,即可得答案;(Ⅱ)过点
,即可得答案;(Ⅱ)过点![]() 作B′E⊥BC,垂足为
作B′E⊥BC,垂足为![]() ,根据矩形的性质可得
,根据矩形的性质可得![]() ,可得
,可得![]() ,即可求出A′C、A′E、B′E的长,进而可得B′点坐标;(Ⅲ)过点
,即可求出A′C、A′E、B′E的长,进而可得B′点坐标;(Ⅲ)过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,可证明
,可证明![]() ,利用勾股定理可求出OB′的长,根据相似三角形的性质可求出OF的长,进而可得A′F的长,即可得点A′坐标.
,利用勾股定理可求出OB′的长,根据相似三角形的性质可求出OF的长,进而可得A′F的长,即可得点A′坐标.
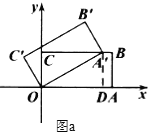
(Ⅰ)如图![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
∵![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() ,即旋转角为
,即旋转角为![]() .
.
(Ⅱ)如图![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
∵![]()
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() 的坐标为
的坐标为![]() .
.
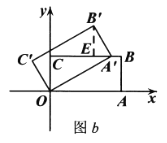
(Ⅲ)如图![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,
∵A′B′=2,A′O=4,
∴B′O=![]() =
=![]() ,
,
∵![]() ,∠A′OB′=∠A′OB′,
,∠A′OB′=∠A′OB′,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴点![]() 的坐标为
的坐标为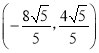 .
.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】在下列选项中,是反比例函数关系的为
A. 在直角三角形中,30°角所对的直角边y与斜边x之间的关系
B. 在等腰三角形中,顶角y与底角x之间的关系
C. 圆的面积S与它的直径d之间的关系
D. 面积为20的菱形,其中一条对角线y与另一条对角线x之间的关系
查看答案和解析>>
科目:初中数学 来源: 题型:
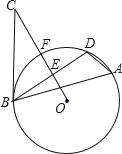
【题目】如图,△ABD是⊙O的内接三角形,E是弦BD的中点,点C是⊙O外一点且∠DBC=∠A,连接OE延长与圆相交于点F,与BC相交于点C.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为6,BC=8,求弦BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组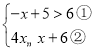 .
.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得_______;
(Ⅱ)解不等式②,得________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
![]()
(Ⅳ)原不等式组的解集为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
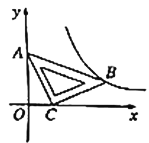
【题目】在平面直角坐标系![]() 中,将一块含有
中,将一块含有![]() 角的直角三角板如图放置,直角顶点
角的直角三角板如图放置,直角顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 恰好落在第一象限的双曲线上,现将直角三角板沿
恰好落在第一象限的双曲线上,现将直角三角板沿![]() 轴正方向平移,当顶点
轴正方向平移,当顶点![]() 恰好落在该双曲线上时停止运动,则此时点
恰好落在该双曲线上时停止运动,则此时点![]() 的对应点
的对应点![]() 的坐标为( )
的坐标为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
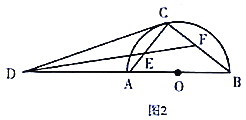
【题目】如图1,![]() 为半圆
为半圆![]() 的直径,
的直径,![]() 为
为![]() 的延长线上一点,
的延长线上一点,![]() 为半圆
为半圆![]() 的切线,切点为
的切线,切点为![]() .
.

(1)求证:![]() ;
;
(2)如图2,![]() 的平分线分别交
的平分线分别交![]() ,
,![]() 于点
于点![]() ,
,![]() .
.
①求![]() 的值;
的值;
②若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“数学迷”小楠通过从“特殊到一般”的过程,对倍角三角形(一个内角是另一个内角的2倍的三角形)进行研究,得出结论:如图1,在![]() 中,
中,![]() 、
、![]() 、
、![]() 的对边分别是
的对边分别是![]() 、
、![]() 、
、![]() ,如果
,如果![]() ,那么
,那么![]() .下面给出小楠对其中一种特殊情形的一种证明方法.
.下面给出小楠对其中一种特殊情形的一种证明方法.
已知:如图2,在△![]() 中,
中,![]() ,
,![]() .求证:
.求证:![]() .
.
证明:如图2,延长![]() 到
到![]() ,使得
,使得![]() .
.
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
又![]() ,
,
∴△![]() △
△![]() .
.
∴![]() ,即
,即![]() .
.
∴![]() .
.
根据上述材料提供的信息,请你完成下列情形的证明(用不同于材料中的方法也可以);
已知:如图1,在△![]() 中,
中,![]() .
.
求证:![]() .
.


查看答案和解析>>
科目:初中数学 来源: 题型:
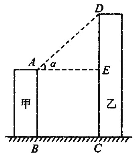
【题目】如图所示.线段AB、DC分别表示甲、乙两座建筑物的高.AB⊥BC,DC⊥BC,两建筑物间距离BC=30米,若甲建筑物高AB=28米,在A点测得D点的仰角α=45°,则乙建筑物高DC=______米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com