
【题目】如图1,![]() 为半圆
为半圆![]() 的直径,
的直径,![]() 为
为![]() 的延长线上一点,
的延长线上一点,![]() 为半圆
为半圆![]() 的切线,切点为
的切线,切点为![]() .
.

(1)求证:![]() ;
;
(2)如图2,![]() 的平分线分别交
的平分线分别交![]() ,
,![]() 于点
于点![]() ,
,![]() .
.
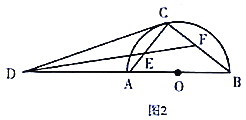
①求![]() 的值;
的值;
②若![]() ,
,![]() ,求
,求![]() 的长.
的长.
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.
(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农经公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:
销售价格x(元/千克) | 30 | 35 | 40 | 45 | 50 |
日销售量p(千克) | 600 | 450 | 300 | 150 | 0 |
(![]() )请你根据表中的数据,写出一个符合p与x的函数表达式__________.
)请你根据表中的数据,写出一个符合p与x的函数表达式__________.
(![]() )农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?
)农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
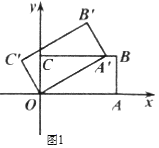
【题目】如图,在平面直角坐标系![]() 中有矩形
中有矩形![]() ,
,![]() ,将矩形
,将矩形![]() 绕原点
绕原点![]() 逆时针旋转得到矩形OA′B′C′.
逆时针旋转得到矩形OA′B′C′.
(Ⅰ)如图1,当点A′首次落在![]() 上时,求旋转角;
上时,求旋转角;
(Ⅱ)在(Ⅰ)的条件下求点B′的坐标;
(Ⅲ)如图2,当点B′首次落在![]() 轴上时,直接写出此时点A′的坐标.
轴上时,直接写出此时点A′的坐标.
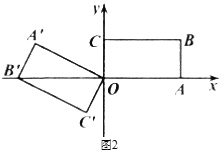
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,BE=EF=FC,CG=2GD,BG分别交AE,AF于M,N.下列结论:①AF⊥BG;②BN=![]() NF;③
NF;③![]() ;④S四边形CGNF=
;④S四边形CGNF=![]() S四边形ANGD.其中正确的结论的序号是 .
S四边形ANGD.其中正确的结论的序号是 .
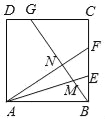
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2﹣2x+3.
(1)把函数关系式配成顶点式并求出图象的顶点坐标和对称轴.
(2)若图象与x轴交点为A.B,与y轴交点为C,求A、B、C三点的坐标;
(3)在图中画出图象.并求出△ABC面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知∠![]() ,点
,点![]() 为射线
为射线![]() 上一点,且
上一点,且![]() ,
,![]() 、
、![]() 为射线
为射线![]() 和
和![]() 上的两个动点(
上的两个动点(![]() ),过点
),过点![]() 作
作![]() ⊥
⊥![]() ,垂足为点
,垂足为点![]() ,且
,且![]() ,联结
,联结![]() .
.
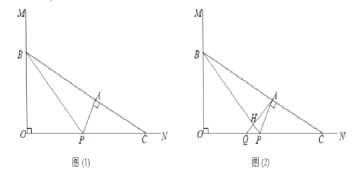
(1)若![]() 时,求
时,求![]() 的值;
的值;
(2)设![]() ,
,![]() 求
求![]() 与
与![]() 之间的函数解析式,并写出定义域;
之间的函数解析式,并写出定义域;
(3)如图(2),过点![]() 作
作![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,交射线
,交射线![]() 于点
于点![]() ,点
,点![]() 、
、![]() 在射线
在射线![]() 和
和![]() 上运动时,探索线段
上运动时,探索线段![]() 的长是否发生变化?若不发生变化,求出它的值。若发生变化,试用含x的代数式表示
的长是否发生变化?若不发生变化,求出它的值。若发生变化,试用含x的代数式表示![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成任务:
自相似图形
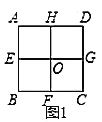
定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:
正方形![]() 中,点
中,点![]() 、
、![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 、
、![]() 边的中点,连接
边的中点,连接![]() ,
,![]() 交于点
交于点![]() ,易知分割成的四个四边形
,易知分割成的四个四边形![]() 、
、![]() 、
、![]() 、
、![]() 均为正方形,且与原正方形相似,故正方形是自相似图形.
均为正方形,且与原正方形相似,故正方形是自相似图形.
任务:
(1)图1中正方形![]() 分割成的四个小正方形中,每个正方形与原正方形的相似比为_______;
分割成的四个小正方形中,每个正方形与原正方形的相似比为_______;
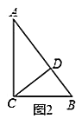
(2)如图2,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,小明发现
,小明发现![]() 也是“自相似图形”,他的思路是:过点
也是“自相似图形”,他的思路是:过点![]() 作
作![]() 于点
于点![]() ,则
,则![]() 将
将![]() 分割成2个与它自己相似的小直角三角形.则
分割成2个与它自己相似的小直角三角形.则![]() 与
与![]() 的相似比为________;则
的相似比为________;则![]() 与
与![]() 的相似比为_______;
的相似比为_______;
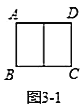
(3)现有一个矩形![]() 是自相似图形,其中长
是自相似图形,其中长![]() ,宽
,宽![]() .
.
①如图3-1,若将矩形![]() 纵向分割成两个全等矩形,且与原矩形都相似,则
纵向分割成两个全等矩形,且与原矩形都相似,则![]() _____(用含
_____(用含![]() 的式子表示);
的式子表示);
②如图3-2若将矩形![]() 纵向分割成
纵向分割成![]() 个全等矩形,且与原矩形都相似,则
个全等矩形,且与原矩形都相似,则![]() ______(用含
______(用含![]() ,
,![]() 的式子表示);
的式子表示);

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=-![]() x+6的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.
x+6的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.

(1)求点B的坐标;
(2)求直线AE的表达式;
(3)过点B作BF⊥AE,垂足为F,连接OF,试判断△OFB的形状,并求△OFB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com