
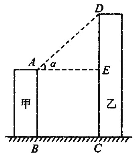
【题目】如图所示.线段AB、DC分别表示甲、乙两座建筑物的高.AB⊥BC,DC⊥BC,两建筑物间距离BC=30米,若甲建筑物高AB=28米,在A点测得D点的仰角α=45°,则乙建筑物高DC=______米.
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,小明按如下步骤作图:
,小明按如下步骤作图:
(1)以点O为圆心,适当长为半径画弧,交OA于D,交OB于点E
(2)分别以点D、E为圆心,大于![]() 的长为半径画弧,两弧在
的长为半径画弧,两弧在![]() 的内部相交于点C
的内部相交于点C
(3)画射线OC
根据上述作图步骤,下列结论正确的有( )个
①射线OC是![]() 的平分线;②点O和点C关于直线DE对称;③射线OC垂直平分线段DE;④
的平分线;②点O和点C关于直线DE对称;③射线OC垂直平分线段DE;④![]() .
.

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块铁皮,拱形边缘呈抛物线状,MN=4,抛物线顶点处到边MN的距离是4,要在铁皮上截下一矩形ABCD,使矩形顶点B、C落在边MN上,A、D落在抛物线上.
(1)如图建立适当的坐标系,求抛物线解析式;
(2)设矩形ABCD的周长为L,点C的坐标为(m,0),求L与m的关系式(不要求写自变量取值范围).
(3)问这样截下去的矩形铁皮的周长能否等于9.5,若不等于9.5,请说明理由,若等于9.5,求出吗的值?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=x2+bx+c(b,c都是常数)的图象经过点(1,0)和(0,2).
(1)当﹣2≤x≤2时,求y的取值范围.
(2)已知点P(m,n)在该函数的图象上,且m+n=1,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中正确的有( ).
①已知任意一边和一个锐角对应相等的两个直角三角形全等.
②任意两角和一边对应相等的两个三角形全等.
③已知任意两边和一角对应相等的两个三角形全等.
④已知腰和顶角对应相等的两个等腰三角形全等.
⑤如果两个三角形有两条边及其中一边上的中线分别相等,那么这两个三角形全等.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作.如图,某探测队在地面A,B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知AB=AC,AB的垂直平分线交AB于点N,交AC于点M,连接MB.
(1)若∠ABC=70°,则∠NMA的度数是 度.
(2)若AB=8cm,△MBC的周长是14cm.
①求BC的长度;
②若点P为直线MN上一点,请你直接写出△PBC周长的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料:一般地,若![]() (
(![]() 且
且![]() ),那么
),那么![]() 叫做以
叫做以![]() 为底
为底![]() 的对数,记作
的对数,记作![]() ,比如指数式
,比如指数式![]() 可以转化为对数式
可以转化为对数式![]() ,对数式
,对数式![]() 可以转化为指数式
可以转化为指数式![]() .
.
根据以上材料,解决下列问题:
(1)计算:![]() ,
,![]() ,
,![]() ;
;
(2)观察(1)中的三个数,猜测:![]() (
(![]() 且
且![]() ,
,![]() ,
,![]() ),并加以证明这个结论;
),并加以证明这个结论;
(3)已知:![]() ,求
,求![]() 和
和![]() 的值(
的值(![]() 且
且![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com