练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】解不等式组.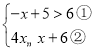

    请结合题意填空，完成本题的解答.

    (Ⅰ)解不等式①，得_______；

    (Ⅱ)解不等式②，得________；

    (Ⅲ)把不等式①和②的解集在数轴上表示出来：

    (Ⅳ)原不等式组的解集为_______.

    【答案】(Ⅰ)；(Ⅱ)；(Ⅲ)见解析；(Ⅳ).

    【解析】

    (Ⅰ)移项即可得答案；(Ⅱ)移项，两边同时除以3即可得答案；(Ⅲ)根据不等式解集的表示方法解答即可；(Ⅳ)根据数轴，找出不等式①②的公共解集即可.

    (Ⅰ)

    移项得：x=-1，

    故答案为：.

    (Ⅱ)

    移项得：3x≤6，

    解得：x≤2，

    故答案为：.

    (Ⅲ)不等式①和②的解集数轴表示如图所示：

    (Ⅳ)由数轴可得①和②的解集的公共解集为x<-1

    ∴原不等式组的解集为.

    故答案为：x<-1

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某物流公司的甲、乙两辆货车分别从A、B两地同时相向而行，并以各自的速度匀速行驶，途径配货站C，甲车先到达C地，并在C地用1小时配货，然后按原速度开往B地，乙车从B地直达A地，下图是甲、乙两车间的距离（千米）与乙车出发（时）的函数的部分图像

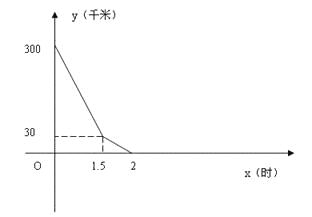
    （1）A、B两地的距离是 千米，甲车出发 小时到达C地；

    （2）求乙车出发2小时后直至到达A地的过程中，与的函数关系式及的取值范围，并在图中补全函数图像；

    （3）乙车出发多长时间，两车相距150千米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：关于x的方程x2+（m-2）x+m-3=0．
    （1）求证：无论m取什么实数，这个方程总有两个不相等的实数根；
    （2）若这个方程的两个实数根x1，x2满足2x1+x2=m+1，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】农经公司以30元/千克的价格收购一批农产品进行销售，为了得到日销售量p（千克）与销售价格x（元/千克）之间的关系，经过市场调查获得部分数据如下表：

    销售价格x（元/千克）

    30

    35

    40

    45

    50

    日销售量p（千克）

    600

    450

    300

    150

    0

    （）请你根据表中的数据，写出一个符合p与x的函数表达式__________．

    （）农经公司应该如何确定这批农产品的销售价格，才能使日销售利润最大？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于二次函数 y=ax2+（b+1）x+（b﹣1），若存在实数 x0，使得当 x=x0，函数 y=x0，则称x0 为该函数的“不变值”.

    （1）当 a=1，b=﹣2 时，求该函数的“不变值”；

    （2）对任意实数 b，函数 y 恒有两个相异的“不变值”，求 a 的取值范围；

    （3）在（2）的条件下，若该图象上 A、B 两点的横坐标是该函数的“不变值”，且 A、B 两点关于直线 y=kx-2a+3 对称，求 b 的最小值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中有矩形，，将矩形绕原点逆时针旋转得到矩形OA′B′C′.

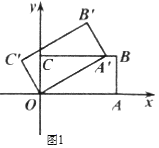
    (Ⅰ)如图1，当点A′首次落在上时，求旋转角；

    (Ⅱ)在(Ⅰ)的条件下求点B′的坐标；

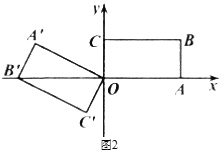
    (Ⅲ)如图2，当点B′首次落在轴上时，直接写出此时点A′的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

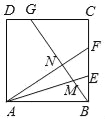
    【题目】如图，正方形ABCD中，BE=EF=FC，CG=2GD，BG分别交AE，AF于M，N．下列结论：①AF⊥BG；②BN=NF；③；④S四边形CGNF=S四边形ANGD．其中正确的结论的序号是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

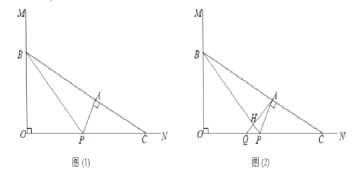
    【题目】如图（1），已知∠,点为射线上一点，且，、为射线和上的两个动点（），过点作⊥，垂足为点，且，联结．

    （1）若时，求的值；

    （2）设，求与之间的函数解析式，并写出定义域；

    （3）如图(2)，过点作的垂线，垂足为点，交射线于点，点、在射线和上运动时，探索线段的长是否发生变化？若不发生变化，求出它的值。若发生变化，试用含x的代数式表示的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知菱形ABCD的周长是48cm， AE⊥BC，垂足为E，AF⊥CD，垂足为F，∠EAF＝2∠C．

    （1）求∠C的度数；

    （2）已知DF的长是关于x的方程x2－5x－a＝0的一个根，求该方程的另一个根．

    查看答案和解析>>

    同步练习册答案