
【题目】已知:关于x的方程x2+(m-2)x+![]() m-3=0.
m-3=0.
(1)求证:无论m取什么实数,这个方程总有两个不相等的实数根;
(2)若这个方程的两个实数根x1,x2满足2x1+x2=m+1,求m的值.
【答案】(1)详见解析;(2)0,![]()
【解析】
(1)△=(m-2)2-4×(![]() m-3)=(m-3)2+7>0,无论m取什么实数,这个方程总有两个不相等的实数根;(2)根据根与系数关系可得:(2m-1)2+(m-2)(2m-1)+
m-3)=(m-3)2+7>0,无论m取什么实数,这个方程总有两个不相等的实数根;(2)根据根与系数关系可得:(2m-1)2+(m-2)(2m-1)+![]() m-3=0.
m-3=0.
(1)证明:△=(m-2)2-4×(![]() m-3),
m-3),
=m2-6m+16,
=(m-3)2+7>0,
∴无论m取什么实数,这个方程总有两个不相等的实数根;
(2)x1+x2=-(m-2),
2x1+x2=x1+(x1+x2)=m+1,
∴x1=m+1+m-2=2m-1,
把x1代入方程有:
(2m-1)2+(m-2)(2m-1)+![]() m-3=0,
m-3=0,
整理得:
6m2-![]() m=0,
m=0,
6m(m-![]() )=0,
)=0,
∴m1=0,m2=![]() .
.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】在一幅长60 cm、宽40 cm的长方形风景画的四周镶一条金色纸边,制成一幅长方形挂图,如图.如果要使整个挂图的面积是2816 cm2,设金色纸边的宽为x cm,那么x满足的方程是( )

A. (60+2x)(40+2x)=2816
B. (60+x)(40+x)=2816
C. (60+2x)(40+x)=2816
D. (60+x)(40+2x)=2816
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民用水实行以户为单位的三级阶梯收费办法:
第一级:居民每户每月用水![]() 吨以内含
吨以内含![]() 吨,每吨收水费
吨,每吨收水费![]() 元;
元;
第二级:居民每户每月用水超过![]() 吨但不超过
吨但不超过![]() 吨,未超过
吨,未超过![]() 的部分按照第一级标准收费,超过部分每吨收水费
的部分按照第一级标准收费,超过部分每吨收水费![]() 元;
元;
第三级:居民每户每月用水超过![]() 吨,未超过
吨,未超过![]() 吨的部分按照第一、二级标准收费,超过部分每吨收水费
吨的部分按照第一、二级标准收费,超过部分每吨收水费![]() 元;
元;
设一户居民月用水![]() 吨,应缴水费
吨,应缴水费![]() 元,
元,![]() 与
与![]() 之间的函数关系如图所示,
之间的函数关系如图所示,
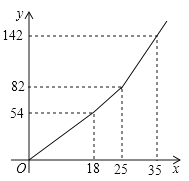
(Ⅰ)根据图象直接作答:![]() ___________,
___________,![]() _______________,
_______________,![]() _______________;
_______________;
(Ⅱ)求当![]() 时,
时,![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(Ⅲ)把上述水费阶梯收费办法称为方案①,假设还存在方案②;居民每户月用水一律按照每吨![]() 元的标准缴费.当居民用户月用水超过
元的标准缴费.当居民用户月用水超过![]() 吨时,请你根据居民每户月用水量的大小设计出对居民缴费最实惠的方案.
吨时,请你根据居民每户月用水量的大小设计出对居民缴费最实惠的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 为直径,C为
为直径,C为![]() 上一点.
上一点.
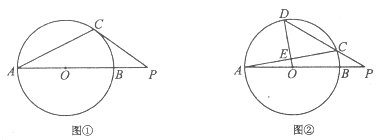
(Ⅰ)如图①,过点C作![]() 的切线,与
的切线,与![]() 的延长线相交于点P,若
的延长线相交于点P,若![]() ,求
,求![]() 的大小;
的大小;
(Ⅱ)如图②,D为弧![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点E,连接
于点E,连接![]() 并延长,与
并延长,与![]() 的延长线相交于点P,若
的延长线相交于点P,若![]() ,求
,求![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列选项中,是反比例函数关系的为
A. 在直角三角形中,30°角所对的直角边y与斜边x之间的关系
B. 在等腰三角形中,顶角y与底角x之间的关系
C. 圆的面积S与它的直径d之间的关系
D. 面积为20的菱形,其中一条对角线y与另一条对角线x之间的关系
查看答案和解析>>
科目:初中数学 来源: 题型:
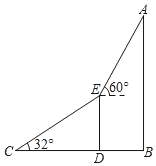
【题目】为庆祝改革开放40周年,深圳举办了灯光秀,某数学兴趣小组为测量“平安金融中心”AB的高度,他们在地面C处测得另一幢大厦DE的顶部E处的仰角∠ECD=32°.登上大厦DE的顶部E处后,测得“平安中心”AB的顶部A处的仰角为60°,(如图).已知C、D、B三点在同一水平直线上,且CD=400米,DB=200米.
(1)求大厦DE的高度;
(2)求平安金融中心AB的高度.
(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组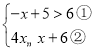 .
.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得_______;
(Ⅱ)解不等式②,得________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
![]()
(Ⅳ)原不等式组的解集为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+1与二次函数y2=ax2+bx﹣2交于A,B两点,且A(1,0)抛物线的对称轴是x=﹣![]() .
.
(1)求k和a、b的值;
(2)求不等式kx+1>ax2+bx﹣2的解集.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com