练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在一幅长60 cm、宽40 cm的长方形风景画的四周镶一条金色纸边，制成一幅长方形挂图，如图.如果要使整个挂图的面积是2816 cm2，设金色纸边的宽为x cm，那么x满足的方程是(　　)

    A. (60＋2x)(40＋2x)＝2816

    B. (60＋x)(40＋x)＝2816

    C. (60＋2x)(40＋x)＝2816

    D. (60＋x)(40＋2x)＝2816

    【答案】A

    【解析】

    根据题意可知，挂画的长和宽分别为（60+2x）cm和(40＋2x)cm，据此可列出方程(60＋2x)(40＋2x)＝2816

    若设金色纸边的宽为x cm，则挂画的长和宽分别为（60+2x）cm和(40＋2x)cm，

    可列方程(60＋2x)(40＋2x)＝2816

    故答案为A.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

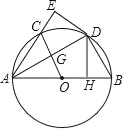
    【题目】如图，Rt△ADB中，∠ADB＝90°，∠DAB＝30°，⊙O为△ADB的外接圆，DH⊥AB于点H，现将△AHD沿AD翻折得到△AED，AE交⊙O于点C，连接OC交AD于点G．

    （1）求证：DE是⊙O的切线；

    （2）若AB＝10，求线段OG的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ACB＝90°，∠B＝4∠BAC．延长BC到点D，使CD＝CB，连接AD，过点D作DE⊥AB于点E，交AC于点F．

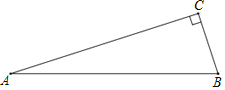
    （1）依题意补全图形；

    （2）求证：∠B＝2∠BAD；

    （3）用等式表示线段EA，EB和DB之间的数量关系，并证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD为矩形，以A为圆心，AD为半径的弧交AB的延长线于点E，连接BD，若AD=2AB=4，则图中阴影部分的面积为______．

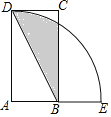
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC与△CDE为等腰直角三角形，∠BAC=∠DEC=90°，连接AD，取AD中点P，连接BP，并延长到点M，使BP=PM，连接AM、EM、AE，将△CDE绕点C顺时针旋转．

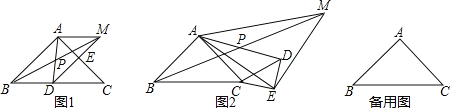
    （1）如图①，当点D在BC上，E在AC上时，AE与AM的数量关系是______，∠MAE=______；

    （2）将△CDE绕点C顺时针旋转到如图②所示的位置，（1）中的结论是否仍然成立，若成立，请给出证明，若不成立，请说明理由；

    （3）若CD=BC，将△CDE由图①位置绕点C顺时针旋转α（0°＜α＜360°），当ME=CD时，请直接写出α的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】选用适当的方法解下列方程

    （1） （2） （3）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】利用配方法解下列方程

    （1） （2）

    （3）

    （4）x（x-4）=2-8x （5）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某物流公司的甲、乙两辆货车分别从A、B两地同时相向而行，并以各自的速度匀速行驶，途径配货站C，甲车先到达C地，并在C地用1小时配货，然后按原速度开往B地，乙车从B地直达A地，下图是甲、乙两车间的距离（千米）与乙车出发（时）的函数的部分图像

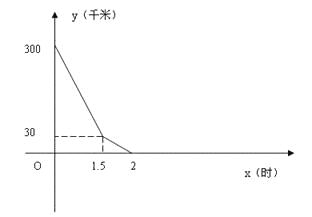
    （1）A、B两地的距离是 千米，甲车出发 小时到达C地；

    （2）求乙车出发2小时后直至到达A地的过程中，与的函数关系式及的取值范围，并在图中补全函数图像；

    （3）乙车出发多长时间，两车相距150千米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：关于x的方程x2+（m-2）x+m-3=0．
    （1）求证：无论m取什么实数，这个方程总有两个不相等的实数根；
    （2）若这个方程的两个实数根x1，x2满足2x1+x2=m+1，求m的值．

    查看答案和解析>>

    同步练习册答案