
����Ŀ��ij������˾�ļס������������ֱ��A��B����ͬʱ������У����Ը��Ե��ٶ�������ʻ��;�����վC���׳��ȵ���C�أ�����C����1Сʱ�����Ȼ��ԭ�ٶȿ���B�أ��ҳ���B��ֱ��A�أ���ͼ�Ǽס���������ľ���![]() ��ǧ�ף����ҳ�����
��ǧ�ף����ҳ�����![]() ��ʱ���ĺ����IJ���ͼ��
��ʱ���ĺ����IJ���ͼ��
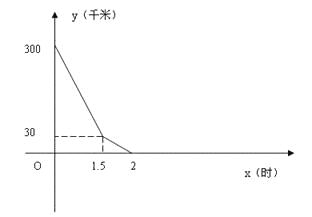
��1��A��B���صľ����� ǧ�ף��׳����� Сʱ����C�أ�
��2�����ҳ�����2Сʱ��ֱ������A�صĹ����У�![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��![]() ��ȡֵ��Χ������ͼ�в�ȫ����ͼ��
��ȡֵ��Χ������ͼ�в�ȫ����ͼ��
��3���ҳ������ʱ�䣬�������150ǧ�ף�
���𰸡���1��300��1.5;��2�� ��3��
��3��![]()
��������
����1��300��1.5; 2��
(2)����֪�����ҵ��ٶ�Ϊ![]() (ǧ��/Сʱ),
(ǧ��/Сʱ),
�����ٶȺ�Ϊ![]() (ǧ��/Сʱ),���Լ��ٶ�Ϊ120ǧ��/Сʱ.
(ǧ��/Сʱ),���Լ��ٶ�Ϊ120ǧ��/Сʱ.
2Сʱ��һʱ�̣�������������2��2.5Сʱ����ͣ�Ҷ���
2.5��3.5Сʱ�����Ҷ��˶���3.5��5Сʱ������ȫ�̣������˶���
��D��2.5,30��,E(3.5,210),F(5,300).
��CD����ʽΪ![]() ,����
,����![]() ,���
,���![]() ��
��![]() ;
;
ͬ��������ã�DE����ʽΪ![]() ��EF����ʽΪ
��EF����ʽΪ![]() .
.
���� . 6��ͼ�����£�
. 6��ͼ�����£�
 7��
7��
��3����![]() ʱ���������AB����ʽΪ
ʱ���������AB����ʽΪ![]() ,
,
��y=150ʱ����![]() Сʱ����
Сʱ����![]() ʱ������
ʱ������![]() ��
��![]() Сʱ��
Сʱ��


 �����ҵ��ٿ���������������ϵ�д�
�����ҵ��ٿ���������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����CD���O�����ڵ�C����AB���ӳ��߽���D��
��1����֤����ADC�ס�CDB��
��2����AC=2��AB=![]() CD�����O�뾶��
CD�����O�뾶��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����60 cm����40 cm�ij����η羰����������һ����ɫֽ�ߣ��Ƴ�һ�������ι�ͼ����ͼ.���Ҫʹ������ͼ�������2816 cm2�����ɫֽ�ߵĿ�Ϊx cm����ôx����ķ�����(����)

A. (60��2x)(40��2x)��2816
B. (60��x)(40��x)��2816
C. (60��2x)(40��x)��2816
D. (60��x)(40��2x)��2816
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����P����������a,b������-2��-1,0,1,2�����������ȡһ������Ϊa��ֵ���ٴ����µ��ĸ�������ȡһ������Ϊb��ֵ�����P��a,b����ƽ��ֱ������ϵ�еڶ������ڵĸ����� .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() ��
��![]() ��
��![]() �IJ��ֶ�Ӧֵ���±���ʾ��
�IJ��ֶ�Ӧֵ���±���ʾ��
| �� | -1 | 0 | 1 | 2 | 3 | 4 | �� |
| �� | 6 | 1 | -2 | -3 | -2 | m | �� |
�������ĸ��۶ϣ�
��������![]() �Ķ���Ϊ
�Ķ���Ϊ![]() ��
��
��![]() ��
��
�۹���![]() �ķ���
�ķ���![]() �Ľ�Ϊ
�Ľ�Ϊ![]() ��
��
��![]() ��
��
���У���ȷ����___________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��B��C��P�ĵ���ڱ߳�Ϊ1��С����������������
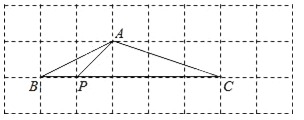
��1���ж���PBA����ABC�Ƿ���������˵��������
��2������BAC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������з��̣�
��1����x��2��2=16
��2��x2��4x��3=0 ���䷽����
��3����x��1����x + 2��= 2��x + 2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�о�����ˮʵ���Ի�Ϊ��λ�����������շѰ취��
��һ��������ÿ��ÿ����ˮ![]() �����ں�
�����ں�![]() �֣�ÿ����ˮ��
�֣�ÿ����ˮ��![]() Ԫ��
Ԫ��
�ڶ���������ÿ��ÿ����ˮ����![]() �ֵ�������
�ֵ�������![]() �֣�δ����
�֣�δ����![]() �IJ��ְ��յ�һ�����շѣ���������ÿ����ˮ��
�IJ��ְ��յ�һ�����շѣ���������ÿ����ˮ��![]() Ԫ��
Ԫ��
������������ÿ��ÿ����ˮ����![]() �֣�δ����
�֣�δ����![]() �ֵIJ��ְ��յ�һ���������շѣ���������ÿ����ˮ��
�ֵIJ��ְ��յ�һ���������շѣ���������ÿ����ˮ��![]() Ԫ��
Ԫ��
��һ����������ˮ![]() �֣�Ӧ��ˮ��
�֣�Ӧ��ˮ��![]() Ԫ��
Ԫ��![]() ��
��![]() ֮��ĺ�����ϵ��ͼ��ʾ��
֮��ĺ�����ϵ��ͼ��ʾ��
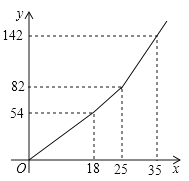
������ͼ��ֱ������![]() ___________��
___________��![]() _______________��
_______________��![]() _______________��
_______________��
������![]() ʱ��
ʱ��![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��������ˮ�ѽ����շѰ취��Ϊ�����٣����軹���ڷ����ڣ�����ÿ������ˮһ�ɰ���ÿ��![]() Ԫ�ı��ɷ�.�������û�����ˮ����
Ԫ�ı��ɷ�.�������û�����ˮ����![]() ��ʱ��������ݾ���ÿ������ˮ���Ĵ�С��Ƴ��Ծ���ɷ���ʵ�ݵķ���.
��ʱ��������ݾ���ÿ������ˮ���Ĵ�С��Ƴ��Ծ���ɷ���ʵ�ݵķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⲻ��ʽ��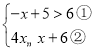 .
.
����������գ���ɱ���Ľ��.
(��)�ⲻ��ʽ�٣���_______��
(��)�ⲻ��ʽ�ڣ���________��
(��)�Ѳ���ʽ�ٺ͢ڵĽ⼯�������ϱ�ʾ������
![]()
(��)ԭ����ʽ��Ľ⼯Ϊ_______.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com