
【题目】已知二次函数![]() ,
,![]() 与
与![]() 的部分对应值如下表所示:
的部分对应值如下表所示:
| … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| … | 6 | 1 | -2 | -3 | -2 | m | … |
下面有四个论断:
①抛物线![]() 的顶点为
的顶点为![]() ;
;
②![]() ;
;
③关于![]() 的方程
的方程![]() 的解为
的解为![]() ;
;
④![]() .
.
其中,正确的有___________________.
【答案】①③.
【解析】
根据图表求出函数对称轴,再根据图表信息和二次函数性质逐一判断即可.
由二次函数y=ax2+bx+c(a≠0),y与x的部分对应值可知:
该函数图象是开口向上的抛物线,对称轴是直线x=2,顶点坐标为(2,-3);与x轴有两个交点,一个在0与1之间,另一个在3与4之间;当y=-2时,x=1或x=3;由抛物线的对称性可知,m=1;
![]() ①抛物线y=ax2+bx+c(a≠0)的顶点为(2,-3),结论正确;
①抛物线y=ax2+bx+c(a≠0)的顶点为(2,-3),结论正确;
②b2﹣4ac=0,结论错误,应该是b2﹣4ac>0;
③关于x的方程ax2+bx+c=﹣2的解为x1=1,x2=3,结论正确;
④m=﹣3,结论错误,
![]() 其中,正确的有. ①③
其中,正确的有. ①③
故答案为:①③


科目:初中数学 来源: 题型:
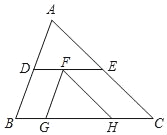
【题目】如图,在△ABC中,D、E分别是边AB、AC上的点,DE∥BC,点F在线段DE上,过点F作FG∥AB、FH∥AC分别交BC于点G、H,如果BG:GH:HC=2:4:3.求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线l和l外一点C.
求作:经过点C且垂直于l的直线.
作法:如图,
(1)在直线l上任取点A;
(2)以点C为圆心,AC为半径作圆,交直线l于点B;
(3)分别以点A,B为圆心,大于![]() 的长为半径作弧,两弧相交于点D;
的长为半径作弧,两弧相交于点D;
(4)作直线CD.
所以直线CD就是所求作的垂线.
(1)请使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:连接AC,BC,AD,BD.
∵AC=BC, = ,
∴CD⊥AB(依据: ).
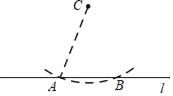
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某研究所将某种材料加热到1000℃时停止加热,并立即将材料分为A、B两组,采用不同工艺做降温对比实验,设降温开始后经过x min时,A、B两组材料的温度分别为yA℃、yB℃,yA、yB与x的函数关系式分别为yA=kx+b,yB=![]() (x﹣60)2+m(部分图象如图所示),当x=40时,两组材料的温度相同.
(x﹣60)2+m(部分图象如图所示),当x=40时,两组材料的温度相同.

(1)分别求yA、yB关于x的函数关系式;
(2)当A组材料的温度降至120℃时,B组材料的温度是多少?
(3)在0<x<40的什么时刻,两组材料温差最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣4x+3.
(1)求该二次函数与x轴的交点坐标和顶点;
(2)在所给坐标系中画出该二次函数的大致图象,并写出当y<0时,x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在测量“河流宽度”的综合与实践活动中,小李同学设计的方案及测量数据如下:在河对岸边选定一个目标点A,在近岸取点B,C,D (点B,C,D在同一条直线上),AB⊥BD,∠ACB=45°,CD=20米,且.若测得∠ADB=25°,请你帮助小李求河的宽度AB.(sin25°≈0.42,cos25°≈0.91,tan25°≈0.47,结果精确到0.1米).

查看答案和解析>>
科目:初中数学 来源: 题型:
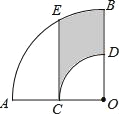
【题目】如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交![]() 于点E,以点O为圆心,OC的长为半径作
于点E,以点O为圆心,OC的长为半径作![]() 交OB于点D.若OA=4,则图中阴影部分的面积为( )
交OB于点D.若OA=4,则图中阴影部分的面积为( )
A. ![]() +
+![]() B.
B. ![]() +2
+2![]() C.
C. ![]() +
+![]() D. 2
D. 2![]() +
+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场,为了吸引顾客,在“白色情人节”当天举办了商品有奖酬宾活动,凡购物满200元者,有两种奖励方案供选择:一是直接获得20元的礼金券,二是得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同,摇奖者必须从摇奖机内一次连续摇出两个球,根据球的颜色(如表)决定送礼金券的多少.
球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 18 | 24 | 18 |
(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率.
(2)如果一名顾客当天在本店购物满200元,若只考虑获得最多的礼品券,请你帮助分析选择哪种方案较为实惠.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com