练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，A、B、C、P四点均在边长为1的小正方形网格格点上．

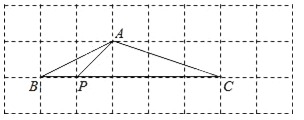
    （1）判断△PBA与△ABC是否相似，并说明理由；

    （2）求∠BAC的度数．

    【答案】（1）相似；（2）135°．

    【解析】试题分析：（1）△PBA与△ABC相似，利用勾股定理计算出AB的长，利用两边对应成比例且一个夹角对应相等的两个三角形相似可证明结论成立；

    （2）由（1）可知：∠BAC=∠BPA，因为∠BPA易求，问题得解．

    试题解析：解：（1）△PBA与△ABC相似．理由如下：

    ∵AB=，BC=5，BP=1，∴．∵∠PBA=∠ABC，∴△PBA∽△ABC；

    （2）∵△PBA∽△ABC，∴∠BAC=∠BPA．∵∠BPA=90°+45°=135°，∴∠BAC=135°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下列各句判定矩形的说法对角线相等的四边形是矩形；对角线互相平分且相等的四边形是矩形；有一个角是直角的四边形是矩形；有四个角是直角的四边形是矩形；四个角都相等的四边形是矩形；对角线相等，且有一个角是直角的四边形是矩形；是正确有几个

    A. 2个 B. 3个 C. 4个 D. 5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知AB是⊙O的直径，点C、D在⊙O上，点E在⊙O外，∠EAC=∠D=60°．

    （1）求∠ABC的度数；

    （2）求证：AE是⊙O的切线；

    （3）当BC=4时，求劣弧AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一方有难八方支援，某市政府筹集抗旱必需物资120吨打算运往灾区，现有甲、乙、丙三种车型可供选择，每辆车的运载能力和运费如下表所示：（假设每辆车均满载）

    (1)若全部物资都用甲、乙两种车来运送，需运费8200元，则分别需甲、乙两种车各几辆？

    (2)为了节约运费，该市政府共调用16辆甲、乙，丙三种车都参与运送物资，试求出有几种运送方案，哪种方案的运费最省？其费用是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了解同学们每月零花钱数额，校园小记者随机调查了本校部分学生，并根据调查结果绘制出如下不完整的统计图表：

    零花钱数额元

    人数（频数）

    频率

    6

    0.15

    12

    0.30

    16

    0.40

    0.10

    2

    请根据以下图表，解答下列问题：

    （1）这次被调查的人数共有__________人，__________；

    （2）计算并补全频数分布直方图；

    （3）请估计该校1500名学生中每月零花钱数额低于90的人数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ACB＝90°，BC的垂直平分线DE交BC于D，交AB于E，F在DE上，并且AF＝CE．

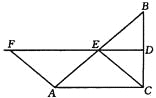
    （1）求证：四边形ACEF是平行四边形；

    （2）当∠B的大小满足什么条件时，四边形ACEF是菱形？请回答并证明你的结论；

    （3）四边形ACEF有可能是正方形吗？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

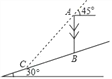
    【题目】如图，在一个坡角为30°的斜坡上有一电线杆AB，当太阳光与水平线成45°角时，测得该杆在斜坡上的影长BC为20m．求电线杆AB的高（精确到0.1m，参考数值：≈1.73，≈1.41）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

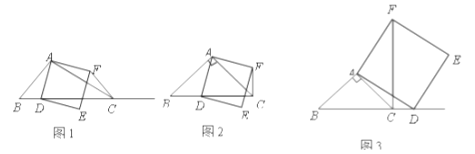
    【题目】如图1，在中，为锐角，点为射线上一点，联结，以为一边且在的右侧作正方形．

    （1）如果，，

    ①当点在线段上时（与点不重合），如图2，线段所在直线的位置关系为 ，线段的数量关系为 ；

    ②当点在线段的延长线上时，如图3，①中的结论是否仍然成立，并说明理由；

    （2）如果，是锐角，点在线段上，当满足什么条件时，（点不重合），并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为准备参加某市2019年度中小学生机器人竞赛，学校对甲、乙两支机器人制作小队所创作的机器人分别从创意、设计、编程与制作三方面进行量化，各项量化满分100分，根据量化结果择优推荐.它们三项量化得分如下表：

    量化项目

    量化得分

    甲队

    乙队

    创意

    85

    72

    设计

    70

    66

    编程与制作

    64

    84

    （1）如果根据三项量化的平均分择优推荐，哪队将被推荐参赛？

    （2）根据本次中小学生机器人竞赛的主题要求，如果学校根据创意、设计、编程与制作三项量化得分按的比例确定每队最后得分的平均分择优推荐，哪队将被推荐参赛？并对另外一队提出合理化的建议.

    查看答案和解析>>

    同步练习册答案