
【题目】如图,△ABC与△CDE为等腰直角三角形,∠BAC=∠DEC=90°,连接AD,取AD中点P,连接BP,并延长到点M,使BP=PM,连接AM、EM、AE,将△CDE绕点C顺时针旋转.
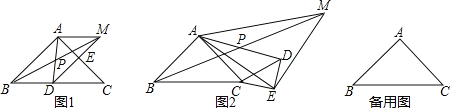
(1)如图①,当点D在BC上,E在AC上时,AE与AM的数量关系是______,∠MAE=______;
(2)将△CDE绕点C顺时针旋转到如图②所示的位置,(1)中的结论是否仍然成立,若成立,请给出证明,若不成立,请说明理由;
(3)若CD=![]() BC,将△CDE由图①位置绕点C顺时针旋转α(0°<α<360°),当ME=
BC,将△CDE由图①位置绕点C顺时针旋转α(0°<α<360°),当ME=![]() CD时,请直接写出α的值.
CD时,请直接写出α的值.
【答案】(1)AM=![]() AE , 45°;(2)成立,见解析;(3)α的值为60°或300°.
AE , 45°;(2)成立,见解析;(3)α的值为60°或300°.
【解析】
(1)证明四边形ABDM是平行四边形即可解决问题.
(2)如图2中,连接BD,DM,BD交AC于点O,交AE于G.证明△BCD∽△ACE,推出∠CBD=∠CAE,![]() =
=![]() ,即可解决问题.
,即可解决问题.
(3)如图2中,首先证明△AEM是等腰直角三角形,分两种情形画出图形分别求解即可.
解:(1)结论:AM=![]() AE,∠MAE=45°.
AE,∠MAE=45°.
理由:如图1中,
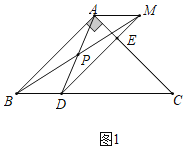
∵AP=PD,BP=PM,
∴四边形ABDM是平行四边形,
∴AM∥BC,
∴∠MAE=∠C,
∵AB=AC,∠BAC=90°,
∴∠C=45°,
∴∠MAE=45°,
∵∠AEM=∠DEC=90°,
∴∠AME=∠EAM=45°,
∴MA=![]() AE.
AE.
故答案为:AM=![]() AE,45°.
AE,45°.
(2)如图2中,连接BD,DM,BD交AC于点O,交AE于G.

∵BC=![]() AC,CD=
AC,CD=![]() CE,
CE,
∴![]() =
=![]() ,
,
∵∠ACB=∠DCE=45°,
∴∠BCD=∠ACE,
∴△BCD∽△ACE,
∴∠CBD=∠CAE,![]() =
=![]() ,
,
∴BD=![]() AE,
AE,
∵∠BOC=∠AOG,
∴∠AGO=∠BCO=45°,
∵AP=PD,BP=PM,
∴四边形ABDM是平行四边形,
∴AM∥BD,AM=BD=![]() AE,
AE,
∴∠MAE=∠BGA=45°,
∵EH⊥AM,
∴△AHE是等腰直角三角形,
∴AH=![]() AE,∵AM=
AE,∵AM=![]() AE,
AE,
∴AH=MH,
∴EA=EM,
∴∠EAM=∠EMA=45°,
∴∠AEM=90°.
(3)如图2中,作EH⊥AM于H.
∵EH⊥AM,∠MAE=45°,
∴△AHE是等腰直角三角形,
∴AH=![]() AE,∵AM=
AE,∵AM=![]() AE,
AE,
∴AH=MH,
∴EA=EM,
∴∠EAM=∠EMA=45°,
∴∠AEM=90°.
如图3-1中,

∵EM=EA=![]() CD,设CD=
CD,设CD=![]() a,则CE=a,BC=2
a,则CE=a,BC=2![]() a,AC=2a,EA=
a,AC=2a,EA=![]() a,
a,
∴AC2=AE2+EC2,
∴∠AEC=90°,
∴tan∠ACE=![]() =
=![]() ,
,
∴∠ACE=60°,
∴旋转角α=60°.
如图3-2中,同法可证∠AEC=90°,∠ACE=60°,此时旋转角α=300°.

综上所述,满足条件的α的值为60°或300°.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,对称轴为直线
,对称轴为直线![]() ,点
,点![]() 是线段
是线段![]() 的中点.
的中点.
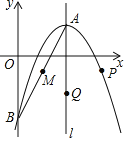
(1)求抛物线的表达式;
(2)写出点![]() 的坐标并求直线
的坐标并求直线![]() 的表达式;
的表达式;
(3)设动点![]() ,
,![]() 分别在抛物线和对称轴l上,当以
分别在抛物线和对称轴l上,当以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形时,求
为顶点的四边形是平行四边形时,求![]() ,
,![]() 两点的坐标.
两点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
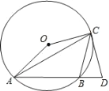
【题目】如图,△ABC是⊙O内接三角形,∠ACB=45°,∠AOC=150°,过点C作⊙O切线交AB延长线于点D.
(1)求证:CD=CB;(2)如果⊙O的半径为![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
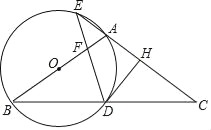
【题目】如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
(1)求证:DH是圆O的切线;
(2)若A为EH的中点,求![]() 的值;
的值;
(3)若EA=EF=1,求圆O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年央视315晚会曝光了卫生不达标的“毒辣条”,“食品安全”受到全社会的广泛关注,“安全教育平台”也推出了“将毒食品拋出窗外”一课我校为了了解九年级家长和学生参“将毒食品抛出窗外”的情况,在我校九年级学生中随机抽取部分学生作调查,把收集的数据分为以下4类情形:
A仅学生自己参与;B.家长和学生一起参与;C仅家长自己参与;D.家长和学生都未参
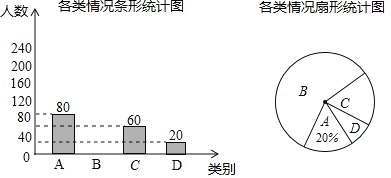
请根据图中提供的信息解答下列问题
(1)在这次抽样调查中,共调查了______名学生
(2)补全条形统计图,并在扇形统计图中计算C类所对应扇形的圆心角的度数
(3)根据抽样调查结果,估计我校九年级2000名学生中“家长和学生都未参与”的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一幅长60 cm、宽40 cm的长方形风景画的四周镶一条金色纸边,制成一幅长方形挂图,如图.如果要使整个挂图的面积是2816 cm2,设金色纸边的宽为x cm,那么x满足的方程是( )

A. (60+2x)(40+2x)=2816
B. (60+x)(40+x)=2816
C. (60+2x)(40+x)=2816
D. (60+x)(40+2x)=2816
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() ,
,![]() 与
与![]() 的部分对应值如下表所示:
的部分对应值如下表所示:
| … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| … | 6 | 1 | -2 | -3 | -2 | m | … |
下面有四个论断:
①抛物线![]() 的顶点为
的顶点为![]() ;
;
②![]() ;
;
③关于![]() 的方程
的方程![]() 的解为
的解为![]() ;
;
④![]() .
.
其中,正确的有___________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 为直径,C为
为直径,C为![]() 上一点.
上一点.
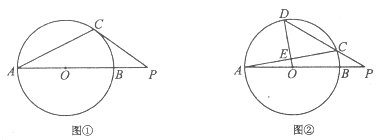
(Ⅰ)如图①,过点C作![]() 的切线,与
的切线,与![]() 的延长线相交于点P,若
的延长线相交于点P,若![]() ,求
,求![]() 的大小;
的大小;
(Ⅱ)如图②,D为弧![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点E,连接
于点E,连接![]() 并延长,与
并延长,与![]() 的延长线相交于点P,若
的延长线相交于点P,若![]() ,求
,求![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com