
【题目】对于二次函数 y=ax2+(b+1)x+(b﹣1),若存在实数 x0,使得当 x=x0,函数 y=x0,则称x0 为该函数的“不变值”.
(1)当 a=1,b=﹣2 时,求该函数的“不变值”;
(2)对任意实数 b,函数 y 恒有两个相异的“不变值”,求 a 的取值范围;
(3)在(2)的条件下,若该图象上 A、B 两点的横坐标是该函数的“不变值”,且 A、B 两点关于直线 y=kx-2a+3 对称,求 b 的最小值.
【答案】(1)-1,3;(2)0<a<1;(3)-![]()
【解析】
(1)先确定二次函数解析式为y=x2-x-3,根据xo是函数y的一个不动点的定义,把(xo,xo)代入得x02-x0-3=xo,然后解此一元二次方程即可;
(2)根据xo是函数y的一个不动点的定义得到axo2+(b+1)xo+(b-1)=xo,整理得ax02+bxo+(b-1)=0,则根据判别式的意义得到△=b2-4a(b-1)>0,即b2-4ab+4a>0,把b2-4ab+4a看作b的二次函数,由于对任意实数b,b2-4ab+4a>0成立,则(4a)2-4.4a<0,然后解此不等式即可.
(3)(利用两点关于直线对称的两个结论,一是中点在已知直线上,二是两点连线和已知直线垂直.找到a,b之间的关系式,整理后在利用基本不等式求解可得.
解:(1)当a=1,b=-2时,二次函数解析式为y=x2-x-3,把(xo,xo)代入得x02-x0-3=xo,解得xo=-1或xo=3,所以函数y的不动点为-1和3;
(2)因为y=xo,所以axo2+(b+1)xo+(b-1)=xo,即ax02+bxo+(b-1)=0,
因为函数y恒有两个相异的不动点,所以此方程有两个不相等的实数解,所以△=b2-4a(b-1)>0,即b2-4ab+4a>0,而对任意实数b,b2-4ab+4a>0成立,所以(4a)2-4.4a<0,解得0<a<1.
(3)设A(x1,x1),B(x2,x2),则x1+x2![]()
A,B的中点的坐标为(![]() ),即M(
),即M(![]() )
)
A、B两点关于直线y=kx-2a+3对称,
又∵A,B在直线y=x上,
∴k=-1,A,B的中点M在直线y=kx-2a+3上.
∴![]() =
=![]() -2a+3 得:b=2a2-3a
-2a+3 得:b=2a2-3a
所以当且仅当a=![]() 时,b有最小值-
时,b有最小值-![]()


科目:初中数学 来源: 题型:
【题目】已知二次函数![]() ,
,![]() 与
与![]() 的部分对应值如下表所示:
的部分对应值如下表所示:
| … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| … | 6 | 1 | -2 | -3 | -2 | m | … |
下面有四个论断:
①抛物线![]() 的顶点为
的顶点为![]() ;
;
②![]() ;
;
③关于![]() 的方程
的方程![]() 的解为
的解为![]() ;
;
④![]() .
.
其中,正确的有___________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 为直径,C为
为直径,C为![]() 上一点.
上一点.
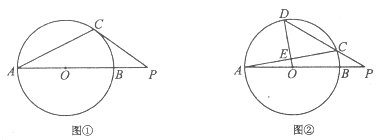
(Ⅰ)如图①,过点C作![]() 的切线,与
的切线,与![]() 的延长线相交于点P,若
的延长线相交于点P,若![]() ,求
,求![]() 的大小;
的大小;
(Ⅱ)如图②,D为弧![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点E,连接
于点E,连接![]() 并延长,与
并延长,与![]() 的延长线相交于点P,若
的延长线相交于点P,若![]() ,求
,求![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
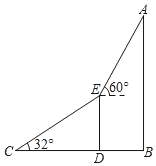
【题目】为庆祝改革开放40周年,深圳举办了灯光秀,某数学兴趣小组为测量“平安金融中心”AB的高度,他们在地面C处测得另一幢大厦DE的顶部E处的仰角∠ECD=32°.登上大厦DE的顶部E处后,测得“平安中心”AB的顶部A处的仰角为60°,(如图).已知C、D、B三点在同一水平直线上,且CD=400米,DB=200米.
(1)求大厦DE的高度;
(2)求平安金融中心AB的高度.
(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形 ABCD 中AB=8![]() ,AD=10,点 E 是 CD 的中点,将这张纸片依次折叠两次: 第一次折叠纸片使点 A 与点 E 重合,如图 2,折痕为 MN,连接 ME、NE;第二次折叠纸片使点 N 与点 E 重合,如图 3,点 B 落到 B′处,折痕为 HG,连接 HE,则下列结论正确的个数是( )①ME∥HG;②△MEH 是等边三角形;③∠EHG=∠AMN;④tan∠EHG=
,AD=10,点 E 是 CD 的中点,将这张纸片依次折叠两次: 第一次折叠纸片使点 A 与点 E 重合,如图 2,折痕为 MN,连接 ME、NE;第二次折叠纸片使点 N 与点 E 重合,如图 3,点 B 落到 B′处,折痕为 HG,连接 HE,则下列结论正确的个数是( )①ME∥HG;②△MEH 是等边三角形;③∠EHG=∠AMN;④tan∠EHG=![]() ;
;

A.1 个B.2 个C.3 个D.4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组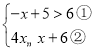 .
.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得_______;
(Ⅱ)解不等式②,得________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
![]()
(Ⅳ)原不等式组的解集为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公园草坪的防护栏由100段形状相同的抛物线形构件组成,为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为( )

A. 50m B. 100m C. 160m D. 200m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产的某种产品每件成本为40元,经市场调查整理出如下信息:
①该产品90天内日销售量(m件)与时间(第x天)满足一次函数关系,部分数据如下表:
时间(第x天) | 1 | 3 | 6 | 10 | … |
日销售量(m件) | 198 | 194 | 188 | 180 | … |
②该产品90天内每天的销售价格与时间(第x天)的关系如下表:
时间(第x天) | 1≤x<50 | 50≤x≤90 |
销售价格(元/件) | x+60 | 100 |
(1)求m关于x的一次函数表达式;
(2)设销售该产品每天利润为y元,请写出y关于x的函数表达式,并求出在90天内该产品哪天的销售利润最大?最大利润是多少?【提示:每天销售利润=日销售量×(每件销售价格-每件成本)】
(3)在该产品销售的过程中,共有多少天销售利润不低于5400元,请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台为了解本地区电视节目的收视情况,对部分市民开展了“你最喜爱的电视节目”的问卷调查(每人只填写一项),根据收集的数据绘制了两幅不完整的统计图(如图所示),根据要求回答下列问题:
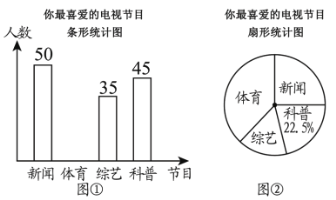
(1)本次问卷调查共调查了________名观众;图②中最喜爱“新闻节目”的人数占调查总人数的百分比为________;
(2)补全图①中的条形统计图;
(3)现有最喜爱“新闻节目”(记为![]() ),“体育节目”(记为
),“体育节目”(记为![]() ),“综艺节目”(记为
),“综艺节目”(记为![]() ),“科普节目”(记为
),“科普节目”(记为![]() )的观众各一名,电视台要从四人中随机抽取两人参加联谊活动,请用列表或画树状图的方法,求出恰好抽到最喜爱“
)的观众各一名,电视台要从四人中随机抽取两人参加联谊活动,请用列表或画树状图的方法,求出恰好抽到最喜爱“![]() ”和“
”和“![]() ”两位观众的概率.
”两位观众的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com