【题目】某公园草坪的防护栏由100段形状相同的抛物线形构件组成，为了牢固起见，每段护栏需要间距0.4m加设一根不锈钢的支柱，防护栏的最高点距底部0.5m（如图），则这条防护栏需要不锈钢支柱的总长度至少为（ ）
A. 50m B. 100m C. 160m D. 200m
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，在平行四边形ABCD，尺规作图：以点A为圆心，AB的长为半径画弧交AD于点F，分别以点B，F为圆心，以大于 BF的长为半径画弧交于点G，做射线AG交BC与点E，若BF=12，AB=10，则AE的长为（ ）．
A.17B.16C.15D.14
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在△ABC中，AB＝AC，D、E是BC边上的点，连接AD、AE，以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E，连接D′C，若BD＝CD′．
（1）求证：△ABD≌△ACD′；
（2）如图2，若∠BAC＝120°，探索BD，DE，CE之间满足怎样的数量关系时，△CD′E是正三角形；
（3）如图3，若∠BAC＝90°，求证：DE2＝BD2+EC2．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读材料（1），并利用（1）的结论解决问题（2）和问题（3）．
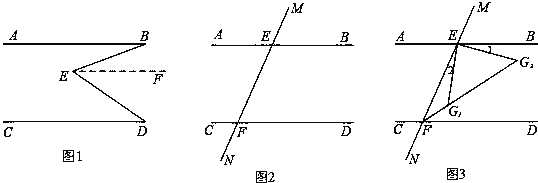
（1）如图1，AB∥CD，E为形内一点，连结BE、DE得到∠BED，求证：∠E＝∠B+∠D
悦悦是这样做的：
过点E作EF∥AB．则有∠BEF＝∠B．
∵AB∥CD，∴EF∥CD．
∴∠FED＝∠D．
∴∠BEF+∠FED＝∠B+∠D．
即∠BED＝∠B+∠D．
（2）如图2，画出∠BEF和∠EFD的平分线，两线交于点G，猜想∠G的度数，并证明你的猜想．
（3）如图3，EG1和EG2为∠BEF内满足∠1＝∠2的两条线，分别与∠EFD的平分线交于点G1和G2，求证：∠FG1E+∠G2＝180°．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，过点D作EF⊥AC于点E，交AB的延长线于点F．
（1）判断直线DE与⊙O的位置关系，并说明理由；
（2）如果AB=5，BC=6，求DE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图1，在平面直角坐标系中，点A，B，E分别是x轴和y轴上的任意点. BD是∠ABE的平分线，BD的反向延长线与∠OAB的平分线交于点C.
探究： （1）求∠C的度数.
发现： （2）当点A，点B分别在x轴和y轴的正半轴上移动时，∠C的大小是否发生变化？若不变，请直接写出结论；若发生变化，请求出∠C的变化范围.
应用：（3）如图2在五边形ABCDE中，∠A＋∠B＋∠E＝310°，CF平分∠DCB，CF的反向延长线与∠EDC外角的平分线相交于点P，求∠P的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园，其中一边靠墙，另外三边由长为30米的篱笆围成．已知墙长为18米（如图所示），设这个苗圃园垂直于墙的一边长为x米．
（1）若苗圃园的面积为72平方米，求x；
（2）若平行于墙的一边长不小于8米，这个苗圃园的面积有最大值和最小值吗？如果有，求出最大值和最小值；如果没有，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
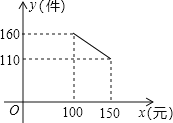
【题目】为发展“低碳经济”，某单位花12500引进了一条环保型生产线生产新产品，在生产过程中，每件产品还需成本40元，物价部门规定该产品售价不得低于100元/件且不得高于150元/件，每月销售量y（件）与销售单价x（元）之间的函数关系如图所示：
（1）求y与x之间的函数关系式，并写出x的取值范围；
（2）第一个月该单位是盈利还是亏损？求出当盈利最大或亏损最小时的产品售价；
（3）在（2）的前提下，即在第一个月盈利最大或亏损最小时，第二个月公司重新确定产品售价，能否使两个月共盈利达10800元？若能，求出第二个月的产品售价；若不能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，若A（﹣4，n），B（2，﹣4）是一次函数y＝kx+b的图象和反比例函数y＝
的图象的两个交点．
（1）求反比例函数和一次函数的解析式；
（2）求直线AB与x轴的交点C的坐标及△AOB的面积；
（3）观察图象，直接写出反比例函数值大于一次函数值x取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
