
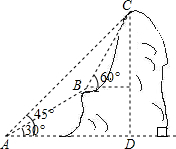
 如图,某电信部门计划修建一条连接B、C两地的电缆.测量人员在山脚A点测得B、C两地的仰角分别为30°、45°,在B地测得C地的仰角为60°.已知C地比A地高200m,电缆BC至少长多少米(精确到1m)?
如图,某电信部门计划修建一条连接B、C两地的电缆.测量人员在山脚A点测得B、C两地的仰角分别为30°、45°,在B地测得C地的仰角为60°.已知C地比A地高200m,电缆BC至少长多少米(精确到1m)? 分析 过B点分别作BE⊥CD、BF⊥AD,垂足分别为E、F.设BC=xm,用x表示出BE、CE,根据题意求出AF、BF,根据正切的定义列出算式,求出x即可.
解答 解:过B点分别作BE⊥CD、BF⊥AD,垂足分别为E、F.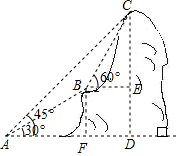
设BC=xm.
∵∠CBE=60°,
∴BE=$\frac{1}{2}$x,CE=$\frac{\sqrt{3}}{2}$x.
∵CD=200,
∴DE=200-$\frac{\sqrt{3}}{2}$x.
∴BF=DE=200-$\frac{\sqrt{3}}{2}$x,DF=BE=$\frac{1}{2}$x.
∵∠CAD=45°,
∴AD=CD=200.
∴AF=200-$\frac{1}{2}$x.
在Rt△ABF中,tan30°=$\frac{BF}{AF}$=$\frac{200-\frac{\sqrt{3}}{2}x}{200-\frac{1}{2}x}$,
解得,x=200($\sqrt{3}$-1)≈147m,
答:电缆BC至少长147米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:选择题
 如图,一条公路的转弯处是一段圆弧(图中的$\widehat{AB}$),点O是这段弧的圆心,C是$\widehat{AB}$上一点,OC⊥AB,垂足为D,AB=160m,CD=40m,则这段弯路的半径是( )
如图,一条公路的转弯处是一段圆弧(图中的$\widehat{AB}$),点O是这段弧的圆心,C是$\widehat{AB}$上一点,OC⊥AB,垂足为D,AB=160m,CD=40m,则这段弯路的半径是( )| A. | 60m | B. | 80m | C. | 100m | D. | 120m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>3 | B. | m≥3 | C. | m≤3 | D. | m<3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
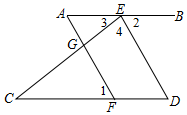 完成下面的推理填空
完成下面的推理填空查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
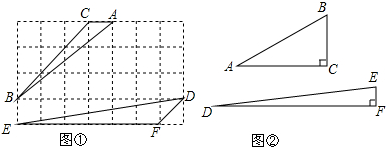
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com