
已知:如图(1),△AOB和△COD都是等边三角形,连接AC、BD交与点P.
(1)求证:AC=BD;
(2)求∠APB的度数;
(3)如图(2),将(1)中的△AOB和△COD改为等腰三角形,并且OA=OB,OC=OD,∠AOB=∠COD=α,则AC与BD的等量关系为 ,∠APB的大小为 .
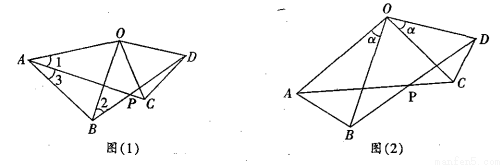
(1) 见解析 (2) 60° (3) AC=BD,∠APB=α
【解析】
试题分析
(1)根据等边三角形性质得出AO=OB,CO=DO,∠AOB=∠COD=60°,求出∠AOC=∠BOD,证出△AOC≌△BOD即可;
(1)根据全等得出∠1=∠2,根据三角形内角和定理求出即可;
(3)求出∠AOC=∠BOD,证出△AOC≌△BOD,推出AC=BD,∠OCA=∠ODB,根据三角形内角和定理求出即可
试题解析:
(1)证明:∵△AOB和△COD都是等边三角形,
∴AO=OB,CO=DO,∠AOB=∠COD=60°,
∴∠AOC=∠BOD=60°+∠BOC,
在△AOC和△BOD中,
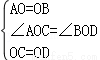 ,
,
∴△AOC≌△BOD(SAS),
∴AC=BD;
(2)【解析】
∵△ABO是等边三角形,
∴∠OAB=∠OBA=60°,
∴∠1+∠3=60°,
∵△AOC≌△BOD,
∴∠1=∠2,
∴∠APB=180°﹣(∠3+∠ABO+∠2)
=180°﹣(∠3+∠1+∠ABO)
=180°﹣(60°+60°)
=60°;
(3)【解析】
AC=BD,∠APB=α,
理由是:∵∠AOB=∠COD=α,
∴∠AOC=∠BOD=∠BOC+α,
在△AOC和△BOD中
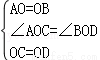
∴△AOC≌△BOD(SAS),
∴AC=BD,∠OCA=∠ODB,
∴∠APB=180°﹣(∠PDC+∠PCO+∠OCD)
=180°﹣(∠PDC+∠BDO+∠OCD)
=180°﹣(∠ODC+∠OCD)
=∠DOC
=α,
故答案为:AC=BD,∠APB=α.
考点:全等三角形的判定与性质;等边三角形的性质


科目:初中数学 来源:2016届江苏省无锡市滨湖区七年级下学期期中考试数学试卷(解析版) 题型:填空题
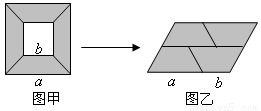
从边长为a的大正方形纸板中挖去一个边长为b的小正方形纸板后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙).那么通过计算两个图形阴影部分的面积,可以验证成立的公式为______________________.
查看答案和解析>>
科目:初中数学 来源:2016届江苏省扬州市七年级下学期期中考试数学试卷(解析版) 题型:解答题
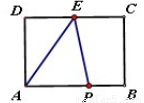
如图,在长方形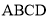 中,
中,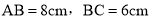 ,点
,点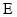 是
是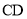 的中点,动点
的中点,动点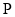 从
从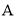 点出发,以每秒
点出发,以每秒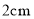 的速度沿
的速度沿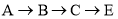 运动,最终到达点
运动,最终到达点 .若设点
.若设点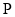 运动的时间是
运动的时间是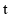 秒,那么当
秒,那么当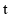 取何值时,△
取何值时,△ 的面积会等于10 ?
的面积会等于10 ?
查看答案和解析>>
科目:初中数学 来源:2016届江苏省张家港市七年级下学期期末调研测试数学试卷(解析版) 题型:解答题
如图,∠E=40°,CD∥AB,∠ABE=2∠ABC,∠BCE=4∠ABC,
(1)若设∠ABC=x°,则∠BCD= °,∠D= °(用含x的代数式表示);
(2)求∠D的度数.

查看答案和解析>>
科目:初中数学 来源:2016届江苏省宜兴市和桥学区七年级下学期期中考试数学试卷(解析版) 题型:解答题
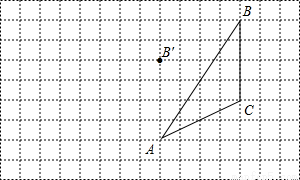
如图,每个小正方形的边长为1,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
(1)补全△A′B′C′根据下列条件,利用网格点和三角板画图:
(2)画出AB边上的中线CD;
(3)画出BC边上的高线AE;
(4)△A′B′C′的面积为 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com