
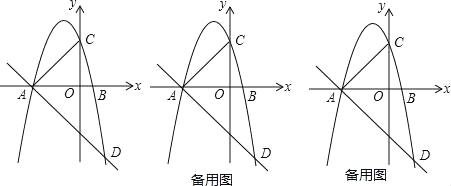
ЁОЬтФПЁПвбжЊХзЮяЯпy=aЃЈx+3ЃЉЃЈxЉ1ЃЉЃЈaЁй0ЃЉЃЌгыxжсДгзѓжСгввРДЮЯрНЛгкAЁЂBСНЕуЃЌгыyжсЯрНЛгкЕуCЃЌОЙ§ЕуAЕФжБЯпy=Љ![]() x+bгыХзЮяЯпЕФСэвЛИіНЛЕуЮЊDЃЎ
x+bгыХзЮяЯпЕФСэвЛИіНЛЕуЮЊDЃЎ
ЃЈ1ЃЉШєЕуDЕФКсзјБъЮЊ2ЃЌЧѓХзЮяЯпЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉШєдкЕкШ§ЯѓЯоФкЕФХзЮяЯпЩЯгаЕуPЃЌЪЙЕУвдAЁЂBЁЂPЮЊЖЅЕуЕФШ§НЧаЮгыЁїABCЯрЫЦЃЌЧѓЕуPЕФзјБъЃЛ
ЃЈ3ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌЩшЕуEЪЧЯпЖЮADЩЯЕФвЛЕуЃЈВЛКЌЖЫЕуЃЉЃЌСЌНгBEЃЎвЛЖЏЕуQДгЕуBГіЗЂЃЌбиЯпЖЮBEвдУПУы1ИіЕЅЮЛЕФЫйЖШдЫЖЏЕНЕуEЃЌдйбиЯпЖЮEDвдУПУы![]() ИіЕЅЮЛЕФЫйЖШдЫЖЏЕНЕуDКѓЭЃжЙЃЌЮЪЕБЕуEЕФзјБъЪЧЖрЩйЪБЃЌЕуQдкећИідЫЖЏЙ§ГЬжаЫљгУЪБМфзюЩйЃП
ИіЕЅЮЛЕФЫйЖШдЫЖЏЕНЕуDКѓЭЃжЙЃЌЮЪЕБЕуEЕФзјБъЪЧЖрЩйЪБЃЌЕуQдкећИідЫЖЏЙ§ГЬжаЫљгУЪБМфзюЩйЃП
ЁОД№АИЁП(1) y=Љ![]() x2Љ2
x2Љ2![]() x+3
x+3![]() ЃЛ(2) PЕФзјБъЮЊЃЈЉ4ЃЌЉ
ЃЛ(2) PЕФзјБъЮЊЃЈЉ4ЃЌЉ![]() ЃЉКЭЃЈЉ6ЃЌЉ
ЃЉКЭЃЈЉ6ЃЌЉ![]() ЃЉЃЛ(3) ЃЈ1ЃЌЉ4
ЃЉЃЛ(3) ЃЈ1ЃЌЉ4![]() ЃЉ.
ЃЉ.
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнЖўДЮКЏЪ§ЕФНЛЕуЪНШЗЖЈЕуAЁЂBЕФзјБъЃЌЧѓГіжБЯпЕФНтЮіЪНЃЌЧѓГіЕуDЕФзјБъЃЌЧѓГіХзЮяЯпЕФНтЮіЪНЃЛЃЈ2ЃЉзїPHЁЭxжсгкHЃЌЩшЕуPЕФзјБъЮЊЃЈmЃЌnЃЉЃЌЗжЁїBPAЁзЁїABCКЭЁїPBAЁзЁїABCЃЌИљОнЯрЫЦШ§НЧаЮЕФаджЪМЦЫуМДПЩЃЛЃЈ3ЃЉзїDMЁЮxжсНЛХзЮяЯпгкMЃЌзїDNЁЭxжсгкNЃЌзїEFЁЭDMгкFЃЌИљОне§ЧаЕФЖЈвхЧѓГіQЕФдЫЖЏЪБМфt=BE+EFЪБЃЌtзюаЁМДПЩЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЁпy=aЃЈx+3ЃЉЃЈxЉ1ЃЉЃЌ
ЁрЕуAЕФзјБъЮЊЃЈЉ3ЃЌ0ЃЉЁЂЕуBСНЕФзјБъЮЊЃЈ1ЃЌ0ЃЉЃЌ
ЁпжБЯпy=Љ![]() x+bОЙ§ЕуAЃЌ
x+bОЙ§ЕуAЃЌ
Ёрb=Љ3![]() ЃЌ
ЃЌ
Ёрy=Љ![]() xЉ3
xЉ3![]() ЃЌ
ЃЌ
ЕБx=2ЪБЃЌy=Љ5![]() ЃЌ
ЃЌ
дђЕуDЕФзјБъЮЊЃЈ2ЃЌЉ5![]() ЃЉЃЌ
ЃЉЃЌ
ЁпЕуDдкХзЮяЯпЩЯЃЌ
ЁрaЃЈ2+3ЃЉЃЈ2Љ1ЃЉ=Љ5![]() ЃЌ
ЃЌ
НтЕУЃЌa=Љ![]() ЃЌ
ЃЌ
дђХзЮяЯпЕФНтЮіЪНЮЊy=Љ![]() ЃЈx+3ЃЉЃЈxЉ1ЃЉ=Љ
ЃЈx+3ЃЉЃЈxЉ1ЃЉ=Љ![]() x2Љ2
x2Љ2![]() x+3
x+3![]() ЃЛ
ЃЛ
ЃЈ2ЃЉзїPHЁЭxжсгкHЃЌ
ЩшЕуPЕФзјБъЮЊЃЈmЃЌnЃЉЃЌ
ЕБЁїBPAЁзЁїABCЪБЃЌЁЯBAC=ЁЯPBAЃЌ
ЁрtanЁЯBAC=tanЁЯPBAЃЌМД![]() =
=![]() ЃЌ
ЃЌ
Ёр![]() =
=![]() ЃЌМДn=ЉaЃЈmЉ1ЃЉЃЌ
ЃЌМДn=ЉaЃЈmЉ1ЃЉЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУЃЌm1=Љ4ЃЌm2=1ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉЃЌ
ЕБm=Љ4ЪБЃЌn=5aЃЌ
ЁпЁїBPAЁзЁїABCЃЌ
Ёр![]() =
=![]() ЃЌМДAB2=ACPBЃЌ
ЃЌМДAB2=ACPBЃЌ
Ёр42=![]()
![]() ЃЌ
ЃЌ
НтЕУЃЌa1=![]() ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉЃЌa2=Љ
ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉЃЌa2=Љ![]() ЃЌ
ЃЌ
дђn=5a=Љ![]() ЃЌ
ЃЌ
ЁрЕуPЕФзјБъЮЊЃЈЉ4ЃЌЉ![]() ЃЉЃЛ
ЃЉЃЛ
ЕБЁїPBAЁзЁїABCЪБЃЌЁЯCBA=ЁЯPBAЃЌ
ЁрtanЁЯCBA=tanЁЯPBAЃЌМД![]() =
=![]() ЃЌ
ЃЌ
Ёр![]() =
=![]() ЃЌМДn=Љ3aЃЈmЉ1ЃЉЃЌ
ЃЌМДn=Љ3aЃЈmЉ1ЃЉЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУЃЌm1=Љ6ЃЌm2=1ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉЃЌ
ЕБm=Љ6ЪБЃЌn=21aЃЌ
ЁпЁїPBAЁзЁїABCЃЌ
Ёр![]() =
=![]() ЃЌМДAB2=BCPBЃЌ
ЃЌМДAB2=BCPBЃЌ
Ёр42=![]()
![]() ЃЌ
ЃЌ
НтЕУЃЌa1=![]() ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉЃЌa2=Љ
ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉЃЌa2=Љ![]() ЃЌ
ЃЌ
дђЕуPЕФзјБъЮЊЃЈЉ6ЃЌЉ![]() ЃЉЃЌ
ЃЉЃЌ
злЩЯЫљЪіЃЌЗћКЯЬѕМўЕФЕуPЕФзјБъЮЊЃЈЉ4ЃЌЉ![]() ЃЉКЭЃЈЉ6ЃЌЉ
ЃЉКЭЃЈЉ6ЃЌЉ![]() ЃЉЃЛ
ЃЉЃЛ
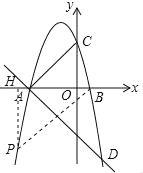
ЃЈ3ЃЉзїDMЁЮxжсНЛХзЮяЯпгкMЃЌзїDNЁЭxжсгкNЃЌзїEFЁЭDMгкFЃЌ
дђtanЁЯDAN=![]() =
=![]() =
=
ЁрЁЯDAN=60ЁуЃЌ
ЁрЁЯEDF=60ЁуЃЌ
ЁрDE=![]() =
=![]() EFЃЌ
EFЃЌ
ЁрQЕФдЫЖЏЪБМфt=![]() +
+![]() =BE+EFЃЌ
=BE+EFЃЌ
ЁрЕБBEКЭEFЙВЯпЪБЃЌtзюаЁЃЌ
дђBEЁЭDMЃЌE(1,Љ4![]() )ЃЎ
)ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєЕЅЯюЪН3x2y5гыЉ2x1Љay3bЉ1ЪЧЭЌРрЯюЃЌЧѓЯТУцДњЪ§ЪНЕФжЕЃК5ab2Љ[6a2bЉ3ЃЈab2+2a2bЃЉ]ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫЎПтЕФЦНОљЫЎЮЛЮЊ80УзЃЌдкДЫЛљДЁЩЯЃЌШєЫЎЮЛБфЛЏЪБЃЌАбЫЎЮЛЩЯЩ§МЧЮЊе§Ъ§ЃЛЫЎПтЙмРэдБМЧТМСЫ3дТЁЋ8дТЫЎЮЛБфЛЏЕФЧщПіЃЈЕЅЮЛЃКУзЃЉЃК-5ЃЌ-4ЃЌ0ЃЌ+3ЃЌ+6ЃЌ+8ЃЎЪдЮЪетМИИідТЕФЪЕМЪЫЎЮЛЪЧЖрЩйУзЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєPЃЈmЃЌnЃЉгыQЃЈnЃЌmЃЉБэЪОЭЌвЛИіЕуЃЌФЧУДетИіЕувЛЖЈдкЃЈ ЃЉ
A. ЕкЖўЁЂЫФЯѓЯо B. ЕквЛЁЂШ§ЯѓЯо C. ЦНаагкxжсЕФжБЯпЩЯ D. ЦНаагкyжсЕФжБЯпЩЯ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊФГЯюЙЄГЬгЩМзввСНЖгКЯзї12ЬьПЩвдЭъГЩ,ЙЉашЙЄГЬЗбгУ13800дЊ,ввЖгЕЅЖРЭъГЩетЯюЙЄГЬЫљашЪБМфЪЧМзЖгЕЅЖРЭъГЩетЯюЙЄГЬЫљашЪБМфЕФ1.5БЖ,ЧвМзЖгУПЬьЕФЙЄГЬЗбгУБШввЖгЖр150дЊЁЃ
ЃЈ1ЃЉМзввСНЖгЕЅЖРЭъГЩетЯюЙЄГЬЗжБ№ашвЊЖрЩйЬь?
ЃЈ2ЃЉШєЙЄГЬЙмРэВПУХОіЖЈДгетСНИіЖгжабЁвЛИіЖгЕЅЖРЭъГЩетЯюЙЄГЬ,ДгНкдМзЪН№ЕФНЧЖШПМТЧ,гІИУбЁдёФФИіЙЄГЬЖг?ЧыЫЕУїРэгЩЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕФкЃЌвбжЊЕуЃЈ1-2aЃЌa-2ЃЉдкЕкШ§ЯѓЯоЕФНЧЦНЗжЯпЩЯЃЌЧѓaЕФжЕМАЕуЕФзјБъЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЕШбќШ§НЧаЮЕФСНБпГЄЗжБ№ЮЊ3cmКЭ6cmЃЌетИіЕШбќШ§НЧаЮЕФжмГЄЮЊ_______cmЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГбЇаЃЮЊСЫНтбЇЩњЖдаТЮХЁЂЬхг§ЁЂЖЏЛЁЂгщРжЁЂЯЗЧњЮхРрЕчЪгНкФПзюЯВАЎЕФЧщПіЃЌЫцЛњЕїВщСЫШєИЩУћбЇЩњЃЌИљОнЕїВщЪ§ОнНјааећРэЃЌЛцжЦСЫШчЯТЕФВЛЭъећЭГМЦЭМЃК

ЧыФуИљОнвдЩЯЕФаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉ БОДЮЙВЕїВщСЫ_____УћбЇЩњЃЌЦфжазюЯВАЎЯЗЧњЕФга_____ШЫЃЛдкЩШаЮЭГМЦЭМжаЃЌзюЯВАЎЬхг§ЕФЖдгІЩШаЮЕФдВаФНЧДѓаЁЪЧ______ЃЛ
ЃЈ2ЃЉ ИљОнвдЩЯЭГМЦЗжЮіЃЌЙРМЦИУаЃ2000УћбЇЩњжазюЯВАЎаТЮХЕФШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com