【题目】点O是△ABC的外心，若∠BOC=80°，则∠BAC的度数为。
【答案】40°或140°
【解析】如图，
点O为△ABC的外心，当点A在A1时，由圆周角定理可知：∠BAC= 
∠BOC=40°；当点A在A2时，∠BAC=180°-∠BA1C=180°-40°=140°；
∴∠BAC的度数为40°或140°.
【考点精析】本题主要考查了圆周角定理和圆内接四边形的性质的相关知识点，需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半；把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线，以相邻切线的交点为顶点的多边形是这个圆的外切正n边形才能正确解答此题．
科目：初中数学 来源： 题型：
【题目】如图，Rt△ABC中，∠ACB=90°，AC边上的垂直平分线交AC于D，交AB于E，延长DE到F，使BF=CE
（1）四边形BCEF是平行四边形吗？说说你的理由．
（2）当∠A等于多少时，四边形BCEF是菱形，并说出你的理由．
（3）四边形BCEF可以是正方形吗？为什么？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在一个
的方格棋盘的
格里放了一枚棋子，如果规定棋子每步只能向上、向下或向左、向右走一格，那么这枚棋子走如下的步数后能到达
格的是（ ）.
A. 7 B. 14 C. 21 D. 28
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，BF为⊙O的直径，直线AC交⊙O于A，B两点，点D在⊙O上，BD平分∠OBC，DE⊥AC于点E．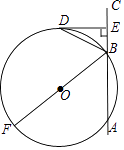
（1）求证：直线DE是⊙O的切线；
（2）若 BF=10，sin∠BDE= 
，求DE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（理解新知）
如图①，已知
，在内部画射线
，得到三个角，分别为
、
、，若这三个角中有一个角是另外一个角的2倍，则称射线为的“2倍角线”
（1）角的平分线 这个角的“2倍角线”；（填“是”或“不是”）
（2）若
，射线为的“2倍角线”，则
；
（解决问题）
如图②，已知
，射线
从
出发，以每秒
的速度绕
点逆时针旋转：射线
从
出发，以每秒
的速度绕点顺时针旋转，射线、同时出发，当一条射线回到出发位置的时候，整个运动随之停止.设运动的时间为
.
(3)当射线、
旋转到同一条直线上时，求
的值；
(4)若、、三条射线中，一条射线恰好是以另外两条射线为边的角的“2倍角线”，直接写出所有可能的的值.（本题中所研究的角都是小于等于
的角.）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在等边△ABC中，AB＝6，N为AB上一点，且AN＝2，∠BAC的平分线交BC于点D，M是AD上的动点，连结BM，MN，则BM+MN的最小值是（ ）
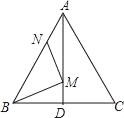
A. 8 B. 10 C. 
D. 2
查看答案和解析>>
科目：初中数学 来源： 题型：
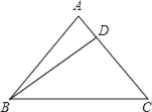
【题目】已知等腰三角形ABC的底边长BC=20cm，D是AC上的一点，且BD=16cm，CD=12cm．
（1）求证：BD⊥AC；
（2）求△ABC的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
