
【题目】如图,Rt△ABC中,∠ACB=90°,AC边上的垂直平分线交AC于D,交AB于E,延长DE到F,使BF=CE
(1)四边形BCEF是平行四边形吗?说说你的理由.
(2)当∠A等于多少时,四边形BCEF是菱形,并说出你的理由.
(3)四边形BCEF可以是正方形吗?为什么?
【答案】
(1)解:四边形BCEF是平行四边形,理由如下:
证明:∵DF垂直且平分AC且∠ACB=90°
∴FD∥BC,AE=CE,
∴∠A=∠ACE,
∵∠A+∠ABC=∠ACE+∠BCE=90°,
∴∠ABC=∠BCE,
∴BE=CE=BF,
∴∠BFE=∠BEF
∵FD∥BC,
∴∠BFE=∠BEF=∠ABC=∠BCE
∴∠FBE=∠BEC,
∴FB∥EC,
∵CE=BF,
∴四边形BCEF为平行四边形;
(2)解:∠A=30°,
证明:∵∠A=30°,
∴∠ABC=60°且BE=CE,
∴△BCE为等边三角形,
∴BC=CE,
由(1)可知四边形BCEF为平行四边形,
∴四边形BCEF为菱形;
(3)解:不可以,
因为∠BCE始终是锐角,所以四边形BCEF不可能是正方形.
【解析】(1)根据已知,先证明FD∥BC得出∠BEF=∠ABC,再根据线段垂直平分线的性质推出∠A=∠ACE,根据等教的余角相等得出∠ABC=∠BCE,证得BE=CE=BF,得出∠BFE=∠BEF,然后证明FB∥EC,即可得出结论。
(2)四边形BCEF是平行四边形,要证明它是菱形,只需证明一组邻边相等,已征得BE=CE,若BC=CE,则BE=BC=CE,即得△BCE为等边三角形,因此∠A=30°。
(3)根据题意可知0°<∠BCE<90°,因此四边形BCEF不可能是正方形。
【考点精析】掌握线段垂直平分线的性质和平行四边形的判定是解答本题的根本,需要知道垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.


科目:初中数学 来源: 题型:
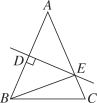
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AC于点E,交AB于点D.
(1)若∠A=40°,求∠CBE的度数;
(2)若△BCE的周长为8cm,AB=5cm,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校准备组织七年级学生参加夏令营,已知:用3辆小客车和1辆大客车每次可运送学生105人;用一辆小客车和2辆大客车每次可运送学生110人,现有学生400人,计划租用小客车a辆,大客车b辆,一次送完,且恰好每辆车都坐满.
(1)1辆小客车和1辆大客车都坐满后一次可送多少名学生?
(2)请你帮学校设计出所有的租车方案;
(3)若小客车每辆需租金200元,大客车每辆需租金380元,请选出最省钱的方案,并求出最省租金.
查看答案和解析>>
科目:初中数学 来源: 题型:
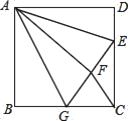
【题目】如图,正方形ABCD中,AB=12,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论: ①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=28.8. 其中正确结论的个数是( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为建设资源节约型、环境友好型社会,克服因干旱而造成的电力紧张困难,切实做好节能减排工作.某地决定对居民家庭用电实行“阶梯电价”,电力公司规定:居民家庭每月用电量在80千瓦时以下(含80千瓦时,1千瓦时俗称1度)时,实行“基本电价”;当居民家庭月用电量超过80千瓦时时,超过部分实行“提高电价”.
(1)小张家今年2月份用电100千瓦时,上缴电费68元;5月份用电120千瓦时,上缴电费88元.求“基本电价”和“提高电价”分别为多少元/千瓦时;
(2)若6月份小张家预计用电130千瓦时,请预算小张家6月份应上缴的电费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如下图, AB∥CD,点E,F分别为AB,CD上一点.
(1) 在AB,CD之间有一点M(点M不在线段EF上),连接ME,MF,试探究∠AEM,∠EMF,∠MFC之间有怎样的数量关系. 请补全图形,并在图形下面写出相应的数量关系,选其中一个进行证明.

(2)如下图,在AB,CD之间有两点M,N,连接ME,MN,NF,请选择一个图形写出∠AEM,∠EMN,∠MNF,∠NFC 存在的数量关系(不需证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OE⊥AB于O,若∠BOD=40°,则不正确的结论是( )

A.∠AOC=40° B.∠COE=130° C.∠EOD=40° D.∠BOE=90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com