
【题目】如图,在△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.求证:BF=2AE.

【答案】证明见解析
【解析】
先判定出△ABD是等腰直角三角形,根据等腰直角三角形的性质可得AD=BD,再根据同角的余角相等求出∠CAD=∠CBE,然后利用“角边角”证明△ADC和△BDF全等,根据全等三角形对应边相等可得BF=AC,再根据等腰三角形三线合一的性质可得AC=2AE,从而得证.
∵AD⊥BC,∠BAD=45°,∴△ABD是等腰直角三角形,∴AD=BD.
∵BE⊥AC,AD⊥BC
∴∠CAD+∠ACD=90°,∠CBE+∠ACD=90°,∴∠CAD=∠CBE.
在△ADC和△BDF中,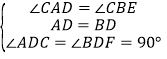 ,∴△ADC≌△BDF(ASA),∴BF=AC.
,∴△ADC≌△BDF(ASA),∴BF=AC.
∵AB=BC,BE⊥AC,∴AC=2AE,∴BF=2AE.


科目:初中数学 来源: 题型:
【题目】黄石市在创建国家级文明卫生城市中,绿化档次不断提升.某校计划购进A,B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A种,B种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,∠B=∠CAD. 
(1)求证:AC是⊙O的切线;
(2)若点E是 ![]() 的中点,连接AE交BC于点F,当BD=5,CD=4时,求AF的值.
的中点,连接AE交BC于点F,当BD=5,CD=4时,求AF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察:从2开始,连续的偶数相加,它们的和的情况如下图:

(1)当加数m的个数为n时,和(S)与n之间有什么样的数量关系,用公式表示出来;
(2)按此规律计算(写出必要的演算过程):
①2+4+6+…+300的值;
②162+164+166+…+400的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC与△CDE都是等边三角形,点B、C、D在同一直线上,AD与BE相交于点G,BE与AC相交于点F,AD与CE相交于点H,则下列结论:①△ACD≌△BCE;②∠AGB=60°;③BF=AH;④△CFH是等边三角形;⑤连CG,则∠BGC=∠DGC ;⑥EG+GC=GD. 其中正确的有________.(只要写序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC边上的垂直平分线交AC于D,交AB于E,延长DE到F,使BF=CE
(1)四边形BCEF是平行四边形吗?说说你的理由.
(2)当∠A等于多少时,四边形BCEF是菱形,并说出你的理由.
(3)四边形BCEF可以是正方形吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(0,4)、C(﹣2,0)在直线l:y=kx+b上,l和函数y=﹣4x+a的图象交于点B
(1)求直线l的表达式;
(2)若点B的横坐标是1,求关于x、y的方程组![]() 的解及a的值.
的解及a的值.
(3)若点A关于x轴的对称点为P,求△PBC的面积.
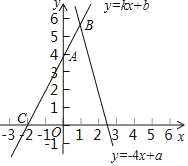
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简再求值:当a=9时,求a+![]() 的值,甲乙两人的解答如下:
的值,甲乙两人的解答如下:
甲的解答为:原式=a+![]() =a+(1-a)=1.
=a+(1-a)=1.
乙的解答为:原式=a+![]() =a+(a-1)=2a-1=17.
=a+(a-1)=2a-1=17.
两种解答中,_____的解答是错误的,错误的原因是当a=9时______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(理解新知)
如图①,已知![]() ,在
,在![]() 内部画射线
内部画射线![]() ,得到三个角,分别为
,得到三个角,分别为![]() 、
、![]() 、
、![]() ,若这三个角中有一个角是另外一个角的2倍,则称射线
,若这三个角中有一个角是另外一个角的2倍,则称射线![]() 为
为![]() 的“2倍角线”
的“2倍角线”
(1)角的平分线 这个角的“2倍角线”;(填“是”或“不是”)
(2)若![]() ,射线
,射线![]() 为
为![]() 的“2倍角线”,则
的“2倍角线”,则![]()
![]() ;
;
(解决问题)
如图②,已知![]() ,射线
,射线![]() 从
从![]() 出发,以每秒
出发,以每秒![]() 的速度绕
的速度绕![]() 点逆时针旋转:射线
点逆时针旋转:射线![]() 从
从![]() 出发,以每秒
出发,以每秒![]() 的速度绕
的速度绕![]() 点顺时针旋转,射线
点顺时针旋转,射线![]() 、
、![]() 同时出发,当一条射线回到出发位置的时候,整个运动随之停止.设运动的时间为
同时出发,当一条射线回到出发位置的时候,整个运动随之停止.设运动的时间为![]() .
.
(3)当射线![]() 、
、![]() 旋转到同一条直线上时,求
旋转到同一条直线上时,求![]() 的值;
的值;
(4)若![]() 、
、![]() 、
、![]() 三条射线中,一条射线恰好是以另外两条射线为边的角的“2倍角线”,直接写出所有可能的
三条射线中,一条射线恰好是以另外两条射线为边的角的“2倍角线”,直接写出所有可能的![]() 的值.(本题中所研究的角都是小于等于
的值.(本题中所研究的角都是小于等于![]() 的角.)
的角.)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com