
【题目】已知点A(0,4)、C(﹣2,0)在直线l:y=kx+b上,l和函数y=﹣4x+a的图象交于点B
(1)求直线l的表达式;
(2)若点B的横坐标是1,求关于x、y的方程组![]() 的解及a的值.
的解及a的值.
(3)若点A关于x轴的对称点为P,求△PBC的面积.
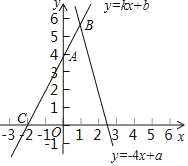
【答案】(1)y=2x+4(2)x=1,y=6; a=10(3)12
【解析】
(1)由于点A、C在直线上,可用待定系数法确定直线l的表达式;
(2)先求出点B的坐标,即得方程组的解.代入组中方程求出a即可;
(3)由于S△BPC=S△PAB+S△PAC,分别求出△PBA和△PAC的面积即可.
(1)由于点A、C在直线l上,
∴![]() ,
,
∴k=2,b=4
所以直线l的表达式为:y=2x+4
(2)由于点B在直线l上,当x=1时,y=2+4=6
所以点B的坐标为(1,6)
因为点B是直线l与直线y=﹣4x+a的交点,
所以关于x、y的方程组![]() 的解为
的解为![]() ,
,
把x=1,y=6代入y=﹣4x+a中,
得a=10;
(3)如图:
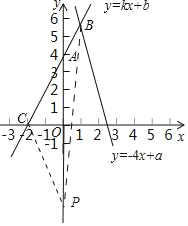
因为点A与点P关于x轴对称,所以点P(0,﹣4),
所以AP=4+4=8,OC=2,
所以S△BPC=S△PAB+S△PAC=![]() ×8×1+
×8×1+![]() ×8×2=4+8=12.
×8×2=4+8=12.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】如图①是某公共汽车线路收支差额y(票价总收入减去运营成本)与乘客量x的函数图象,目前这条线路亏损,为了扭亏,有关部门举行提高票价的听证会,乘客代表认为:公交公司应降低运营成本,实现扭亏,公交公司认为:运营成本难以下降,提高票价才能扭亏根据这两种意见,把图①分别改画成图②和图③.则下列判断不合理的是( )

A. 图①中点A的实际意义是公交公司运营后亏损1万元
B. 图①中点B的实际意义是乘客量为1.5万时公交公司收支平衡
C. 图②能反映公交公司意见
D. 图③能反映乘客意见
查看答案和解析>>
科目:初中数学 来源: 题型:
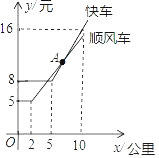
【题目】如图表示某公司“顺风车”与“快车”的行驶里程x(千米)与计费y(元)之间的函数图象.
(1)由图象写出乘车里程为5千米时选择 (“顺风车”或“快车”)更便宜;
(2)当x>5时,顺风车的函数是y=![]() x+
x+![]() ,判断乘车,里程是8千米时,选择“顺风车”和“快车”哪个更便宜?说明理由.
,判断乘车,里程是8千米时,选择“顺风车”和“快车”哪个更便宜?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如下图, AB∥CD,点E,F分别为AB,CD上一点.
(1) 在AB,CD之间有一点M(点M不在线段EF上),连接ME,MF,试探究∠AEM,∠EMF,∠MFC之间有怎样的数量关系. 请补全图形,并在图形下面写出相应的数量关系,选其中一个进行证明.

(2)如下图,在AB,CD之间有两点M,N,连接ME,MN,NF,请选择一个图形写出∠AEM,∠EMN,∠MNF,∠NFC 存在的数量关系(不需证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表中有两种移动电话计费方式:
月使用费(元) | 主叫限定时间(分钟) | 主叫超时费(元/分钟) | 被叫 | |
方式一 | 65 | 160 | 0.25 | 免费 |
方式二 | 100 | 380 | 0.19 | 免费 |
说明:月使用费固定收取,主叫不超限定时间不再收费,主叫超时部分加收超时费;被叫免费.
(1)若李杰某月主叫通话时间为200分钟则他按方式一计费需 元,按方式二计费需 元;若他按方式二计费需103.8元,则主叫通话时间为 分钟;
(2)是否存在某主叫通话时间t(分钟),按方式一和方式二的计费相等,若存在,请求出t的值;若不存在,请说明理由;
(3)请你通过计算分析后,直接给出当月主叫通话时间t(分钟)满足什么条件时,选择方式一省钱;当每月主叫通话时间t(分钟)满足什么条件时,选择方式二省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
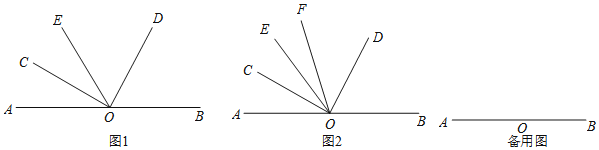
【题目】点O为直线AB上一点,在直线AB上侧任作一个∠COD,使得∠COD=90°.
(1)如图1,过点O作射线OE,当OE恰好为∠AOD的角平分线时,请直接写出∠BOD与∠COE之间的倍数关系,即∠BOD= ______ ∠COE(填一个数字);
(2)如图2,过点O作射线OE,当OC恰好为∠AOE的角平分线时,另作射线OF,使得OF平分∠COD,求∠FOB+∠EOC的度数;
(3)在(2)的条件下,若∠EOC=3∠EOF,求∠AOE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com