
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围.
【答案】
(1)解:根据题意得:(30﹣2x)x=72,
解得:x=3,x=12,
∵30﹣2x≤18,
∴x=12;
(2)解:设苗圃园的面积为y,
∴y=x(30﹣2x)=﹣2x2+30x,
∵a=﹣2<0,
∴苗圃园的面积y有最大值,
∴当x= ![]() 时,即平行于墙的一边长15>8米,y最大=112.5平方米;
时,即平行于墙的一边长15>8米,y最大=112.5平方米;
∵6≤x≤11,
∴当x=11时,y最小=88平方米;
(3)解:由题意得:﹣2x2+30x≥100,
∵30﹣2x≤18
解得:6≤x≤10.
【解析】(1)根据苗圃园的面积=72平方米,垂直于墙的一边的长![]() 2+平行于墙的一边长=30,设未知数建立方程求解,再根据30﹣2x≤18,求出x的取值范围,即可得出符合条件的x的值。
2+平行于墙的一边长=30,设未知数建立方程求解,再根据30﹣2x≤18,求出x的取值范围,即可得出符合条件的x的值。
(2)设苗圃园的面积为y,建立y与x的函数关系式,再根据8,8≤30﹣2x≤18,求出自变量的取值范围,根据二次函数的性质,求出结果。
(3)根据这个苗圃园的面积≥100及30﹣2x≤18,即可求解。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,∠B=∠CAD. 
(1)求证:AC是⊙O的切线;
(2)若点E是 ![]() 的中点,连接AE交BC于点F,当BD=5,CD=4时,求AF的值.
的中点,连接AE交BC于点F,当BD=5,CD=4时,求AF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(0,4)、C(﹣2,0)在直线l:y=kx+b上,l和函数y=﹣4x+a的图象交于点B
(1)求直线l的表达式;
(2)若点B的横坐标是1,求关于x、y的方程组![]() 的解及a的值.
的解及a的值.
(3)若点A关于x轴的对称点为P,求△PBC的面积.
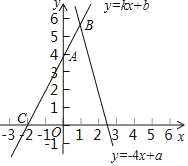
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简再求值:当a=9时,求a+![]() 的值,甲乙两人的解答如下:
的值,甲乙两人的解答如下:
甲的解答为:原式=a+![]() =a+(1-a)=1.
=a+(1-a)=1.
乙的解答为:原式=a+![]() =a+(a-1)=2a-1=17.
=a+(a-1)=2a-1=17.
两种解答中,_____的解答是错误的,错误的原因是当a=9时______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是长方形纸带,将纸带沿EF折叠成图2,再沿BF折叠成图3.
(1)若∠DEF=20°,则图3中∠CFE度数是多少?
(2)若∠DEF=a,把图3中∠CFE用a表示.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个![]() 的方格棋盘的
的方格棋盘的![]() 格里放了一枚棋子,如果规定棋子每步只能向上、向下或向左、向右走一格,那么这枚棋子走如下的步数后能到达
格里放了一枚棋子,如果规定棋子每步只能向上、向下或向左、向右走一格,那么这枚棋子走如下的步数后能到达![]() 格的是( ).
格的是( ).

A. 7 B. 14 C. 21 D. 28
查看答案和解析>>
科目:初中数学 来源: 题型:
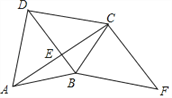
【题目】如图,四边形ABCD的对角线AC⊥BD于点E,AB=BC,F为四边形ABCD外一点,且∠FCA=90°,∠CBF=∠DCB.
(1)求证:四边形DBFC是平行四边形;
(2)如果BC平分∠DBF,∠CDB=45°,BD=2,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(理解新知)
如图①,已知![]() ,在
,在![]() 内部画射线
内部画射线![]() ,得到三个角,分别为
,得到三个角,分别为![]() 、
、![]() 、
、![]() ,若这三个角中有一个角是另外一个角的2倍,则称射线
,若这三个角中有一个角是另外一个角的2倍,则称射线![]() 为
为![]() 的“2倍角线”
的“2倍角线”
(1)角的平分线 这个角的“2倍角线”;(填“是”或“不是”)
(2)若![]() ,射线
,射线![]() 为
为![]() 的“2倍角线”,则
的“2倍角线”,则![]()
![]() ;
;
(解决问题)
如图②,已知![]() ,射线
,射线![]() 从
从![]() 出发,以每秒
出发,以每秒![]() 的速度绕
的速度绕![]() 点逆时针旋转:射线
点逆时针旋转:射线![]() 从
从![]() 出发,以每秒
出发,以每秒![]() 的速度绕
的速度绕![]() 点顺时针旋转,射线
点顺时针旋转,射线![]() 、
、![]() 同时出发,当一条射线回到出发位置的时候,整个运动随之停止.设运动的时间为
同时出发,当一条射线回到出发位置的时候,整个运动随之停止.设运动的时间为![]() .
.
(3)当射线![]() 、
、![]() 旋转到同一条直线上时,求
旋转到同一条直线上时,求![]() 的值;
的值;
(4)若![]() 、
、![]() 、
、![]() 三条射线中,一条射线恰好是以另外两条射线为边的角的“2倍角线”,直接写出所有可能的
三条射线中,一条射线恰好是以另外两条射线为边的角的“2倍角线”,直接写出所有可能的![]() 的值.(本题中所研究的角都是小于等于
的值.(本题中所研究的角都是小于等于![]() 的角.)
的角.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角△ABC内接于⊙O,点D是直角△ABC斜边AB上的一点,过点D作AB的垂线交AC于E,过点C作∠ECP=∠AED,CP交DE的延长线于点P,连结PO交⊙O于点F.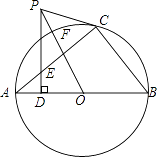
(1)求证:PC是⊙O的切线;
(2)若PC=3,PF=1,求AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com