
【题目】如图,直角△ABC内接于⊙O,点D是直角△ABC斜边AB上的一点,过点D作AB的垂线交AC于E,过点C作∠ECP=∠AED,CP交DE的延长线于点P,连结PO交⊙O于点F.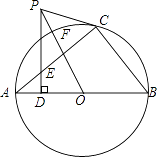
(1)求证:PC是⊙O的切线;
(2)若PC=3,PF=1,求AB的长.
【答案】
(1)解:如图,连接OC,
∵PD⊥AB,
∴∠ADE=90°,
∵∠ECP=∠AED,
又∵∠EAD=∠ACO,
∴∠PCO=∠ECP+∠ACO=∠AED+∠EAD=90°,
∴PC⊥OC,
∴PC是⊙O切线
(2)解:解法一:
延长PO交圆于G点,
∵PF×PG=PC2,PC=3,PF=1,
∴PG=9,
∴FG=9﹣1=8,
∴AB=FG=8.
解法二:
设⊙O的半径为x,则OC=x,OP=1+x
∵PC=3,且OC⊥PC
∴32+x2=(1+x)2
解得x=4
∴AB=2x=8
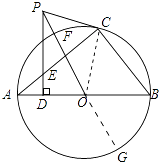
【解析】(1)连接OC,欲证明PC是⊙O的切线,只要证明PC⊥OC即可.(2)延长PO交圆于G点,由切割线定理求出PG即可解决问题.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点O为直线AB上一点,在直线AB上侧任作一个∠COD,使得∠COD=90°.
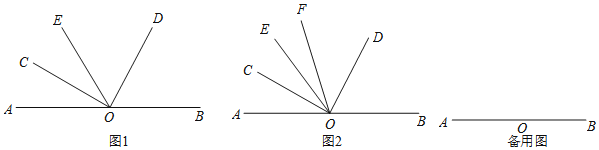
(1)如图1,过点O作射线OE,当OE恰好为∠AOD的角平分线时,请直接写出∠BOD与∠COE之间的倍数关系,即∠BOD= ______ ∠COE(填一个数字);
(2)如图2,过点O作射线OE,当OC恰好为∠AOE的角平分线时,另作射线OF,使得OF平分∠COD,求∠FOB+∠EOC的度数;
(3)在(2)的条件下,若∠EOC=3∠EOF,求∠AOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,P,Q分别是BC,AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R,S,若AQ=PQ,PR=PS,下面三个结沦:①AS=AR:②QP∥AR;③△BRP≌△CSP.其中正确的是( )

A. ①③ B. ②③ C. ①② D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
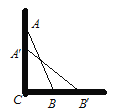
【题目】一架长2.5米的梯子AB如图所示斜靠在一面墙上,这时梯足B离墙底C(∠C=90°)的距离BC为0.7米.
(1)求此时梯顶A距地面的高度AC;
(2)如果梯顶A下滑0.9米,那么梯足B在水平方向,向右滑动了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的是一种盛装葡萄酒的瓶子,现量得瓶塞AB与标签CD的高度之比为2:3,且瓶子底部DE=![]() AB,点C是BD的中点,又量得AE=300mm,设DE的长为
AB,点C是BD的中点,又量得AE=300mm,设DE的长为![]()
(1)用含![]() 的式于直接表示出AB、BC的长;
的式于直接表示出AB、BC的长;
(2)求标签CD的高度。
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒,连接DE,当△BDE是直角三角形时,t的值______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
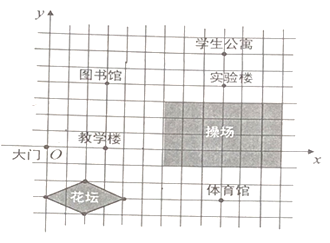
【题目】(1)如图,是某学校的平面简图,以学校大门位置为坐标原点建立平面直角坐标系.写出图中教学楼、图书馆、体育馆、实验楼、学生公寓位置的坐标(网格小正方形的边长记为1个长度单位).
教学楼:_____________;
图书馆:_____________;
体育馆:_____________;
实验楼:_____________;
学生公寓:_____________;
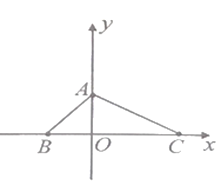
(2)点![]() 在坐标系中的位置如图所示,三角形
在坐标系中的位置如图所示,三角形![]() 的面积为
的面积为![]()
①三角形![]() 三个顶点的坐标分别为:
三个顶点的坐标分别为:![]() (____,____),
(____,____),![]() (____,_____),
(____,_____),![]() (__,__);
(__,__);
②点![]() 是一动点,若三角形
是一动点,若三角形![]() 面积等于三角形
面积等于三角形![]() 面积.求点
面积.求点![]() 坐标.
坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
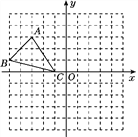
【题目】如图,已知网格上最小的正方形的边长为1.
(1)分别写出A,B,C三点的坐标;
(2)作△ABC关于y轴的对称图形△A′B′C′(不写作法),想一想:关于y轴对称的两个点之间有什么关系?
(3)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com