Question

【题目】已知：如下图， AB∥CD，点E，F分别为AB，CD上一点.

（1） 在AB，CD之间有一点M（点M不在线段EF上），连接ME，MF，试探究∠AEM，∠EMF，∠MFC之间有怎样的数量关系. 请补全图形，并在图形下面写出相应的数量关系，选其中一个进行证明.

（2）如下图，在AB，CD之间有两点M，N，连接ME，MN，NF，请选择一个图形写出∠AEM，∠EMN，∠MNF，∠NFC 存在的数量关系（不需证明）.

Answer 1

【答案】（1）∠EMF＝∠AEM＋∠MFC，∠AEM＋∠EMF＋∠MFC＝360°（2）第一图数量关系：∠EMN＋∠MNF－∠AEM－∠NFC＝180°.第二图数量关系：∠EMN－∠MNF＋∠AEM＋∠NFC＝180°.

【解析】试题分析：(1)分点M在EF的左侧和右侧两种情况，当点M在EF的左侧时，如图，∠EMF＝∠AEM＋∠MFC，过点M作MP∥AB，可得AB∥CD∥MP， 根据平行线的性质可得∠4＝∠3， ∠1＝∠2，即可证得∠EMF＝∠AEM＋∠MFC；当点M在EF的右侧时，类比左侧的方法即可证得∠AEM＋∠EMF＋∠MFC＝360°；（2）类比（1）的方法作平行线，利用平行线的性质即可解决.

试题解析：

（1）∠EMF＝∠AEM＋∠MFC.

证明：过点M作MP∥AB.

∵AB∥CD，

∴MP∥CD.

∴∠4＝∠3.

∵MP∥AB，

∴∠1＝∠2.

∵∠EMF＝∠2＋∠3，

∴∠EMF＝∠1＋∠4.

∴∠EMF＝∠AEM＋∠MFC.

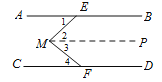
∠AEM＋∠EMF＋∠MFC＝360°

证明：过点M作MQ∥AB.

∵AB∥CD，

∴MQ∥CD.

∴∠CFM＋∠1＝180°.

∵MQ∥AB，

∴∠AEM＋∠2＝180°.

∴∠CFM＋∠1+∠AEM＋∠2＝360°

∵∠EMF＝∠1＋∠2

∴∠AEM＋∠EMF＋∠MFC＝360°.

（2）第一图数量关系：∠EMN＋∠MNF－∠AEM－∠NFC＝180°.

第二图数量关系：∠EMN－∠MNF＋∠AEM＋∠NFC＝180°.