
【题目】如图,顺次连接矩形ABCD四边的中点得到四边形A1B1C1D1,然后顺次连接四边形A1B1C1D1的中点得到四边形A2B2C2D2,再顺次连接四边形A2B2C2D2四边的中点得到四边形A3B3C3D3,…,已知AB=6, BC=8,按此方法得到的四边形A5B5C5D5的周长为(______).

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知:如下图, AB∥CD,点E,F分别为AB,CD上一点.
(1) 在AB,CD之间有一点M(点M不在线段EF上),连接ME,MF,试探究∠AEM,∠EMF,∠MFC之间有怎样的数量关系. 请补全图形,并在图形下面写出相应的数量关系,选其中一个进行证明.

(2)如下图,在AB,CD之间有两点M,N,连接ME,MN,NF,请选择一个图形写出∠AEM,∠EMN,∠MNF,∠NFC 存在的数量关系(不需证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自学:如图1,△ABC中,D是BC边上一点,则△ABD与△ADC有一个相同的高,它们的面积之比等于相应的底之比,记为 ![]() =
= ![]() .
.
(△ABD,△ADC的面积分别用记号S△ABD , S△ADC表示)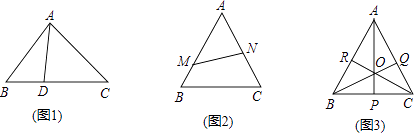
(1)心得:如图1,若BD= ![]() DC,则S△ABD:S△ADC=
DC,则S△ABD:S△ADC=
(2)成长:如图2,△ABC中,M,N分别是AB,AC边上一点,且有AM:MB=2:1,AN:NC=1:1,则△AMN与△ABC的面积比为 .
(3)巅峰:如图3,△ABC中,P,Q,R分别是BC,CA,AB边上的点,且AP,BQ,CR相交于点O,现已知△BPO,△PCO,△COQ,△AOR的面积依次为40,30,35,84,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】6月5日是“世界环境日”,某校从3名男生和2名女生中随机抽取学生去参加市中学生环保演讲比赛.
(1)若抽取1名学生参加,恰好是男生的概率是;
(2)如果抽取1名学生参加,请用列表或树状图求出恰好是1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为6,B是数轴上一点,且
![]() .动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(
.动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(![]() )秒.
)秒.
![]()
(1)请写出数轴上点B表示的数 ,点P表示的数 (用含t 的整式表示);
(2)若M为AP的中点,N为PB的中点.点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明有5张写着不同的数字的卡片,请你按要求抽出卡片,完成下列各问题:
![]()
(1)从中取出2张卡片,使这2张卡片上数字乘积最大,最大值是 ;
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,最小值是 ;
(3)从中取出4张卡片,用学过的运算方法,使结果为24.写出运算式子:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面我们做一次折叠活动:
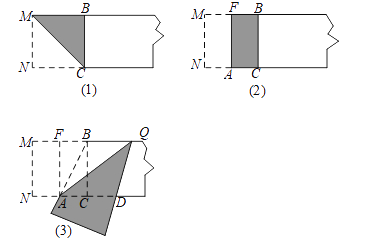
第一步,在一张宽为2的矩形纸片的一端,利用图(1)的方法折出一个正方形,然后把纸片展平,折痕为MC;
第二步,如图(2),把这个正方形折成两个相等的矩形,再把纸片展平,折痕为FA;
第三步,折出内侧矩形FACB的对角线AB,并将AB折到图(3)中所示的AD处,折痕为AQ.
根据以上的操作过程,完成下列问题:
(1)求CD的长.
(2)请判断四边形ABQD的形状,并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(-6)-(-9); (2)1.8-(-2.6);
(3)![]() ; (4)8-(9-10);
; (4)8-(9-10);
(5)(-61)-(-71)-(-8)-(-2); (6)![]() -3.7-(-
-3.7-(-![]() )-1.3.
)-1.3.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com