
【题目】自学:如图1,△ABC中,D是BC边上一点,则△ABD与△ADC有一个相同的高,它们的面积之比等于相应的底之比,记为 ![]() =
= ![]() .
.
(△ABD,△ADC的面积分别用记号S△ABD , S△ADC表示)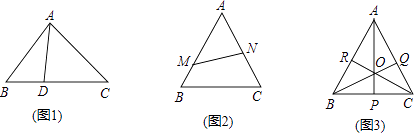
(1)心得:如图1,若BD= ![]() DC,则S△ABD:S△ADC=
DC,则S△ABD:S△ADC=
(2)成长:如图2,△ABC中,M,N分别是AB,AC边上一点,且有AM:MB=2:1,AN:NC=1:1,则△AMN与△ABC的面积比为 .
(3)巅峰:如图3,△ABC中,P,Q,R分别是BC,CA,AB边上的点,且AP,BQ,CR相交于点O,现已知△BPO,△PCO,△COQ,△AOR的面积依次为40,30,35,84,求△ABC的面积.
【答案】
(1)1:2
(2)1:3
(3)
解:设△BRO和△AOQ的面积分别为x、y,
∵△BPO,△PCO的面积分别为40,30,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
![]() =2,
=2,
∴OB=2OQ,
∴ ![]() =2,即
=2,即 ![]() =2,
=2,
则 ![]() ,
,
解得, ![]() ,
,
∴△ABC的面积为:40+30+35+84+60+72=321
【解析】解:心得:∵BD= ![]() DC,
DC,
∴ ![]() =
= ![]() ,
,
∴S△ABD:S△ADC=1:2,
所以答案是:1:2;
成长:如图②.连接BN,
∵AN:NC=1:1,
∴S△ANB=S△CNB= ![]() S△ABC ,
S△ABC ,
∵AM:MB=2:1,
∴SAMN= ![]() S△ANB ,
S△ANB ,
∴△AMN与△ABC的面积比为1:3,
所以答案是:1:3;
巅峰: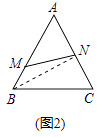
【考点精析】本题主要考查了相似三角形的应用的相关知识点,需要掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解才能正确解答此题.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】某牛奶厂在一条南北走向的大街上设有O,A,B,C四家特约经销店.A店位于O店的南面3千米处;B店位于O店的北面1千米处,C店在O店的北面2千米处.
(1)请以O为原点,向北的方向为正方向,1个单位长度表示1千米,画一条数轴,你能在数轴上分别表示出O,A,B,C的位置吗?
(2)牛奶厂的送货车从O店出发,要把一车牛奶分别送到A,B,C三家经销店,那么送货车走的最短路程是多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知小正方形 ABCD 的面积为1,把它的各边延长一倍得到新正方形 A 1 B 1 C 1 D 1 ;把正方形 A 1 B 1 C 1 D 1 边长按原法延长一倍得到正方形 A 2 B 2 C 2 D 2 (如图(2));以此下去,则正方形 A n B n C n D n 的面积为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅游团上午6时从旅馆出发,乘汽车到距离210km的某著名旅游景点游玩,该汽车离旅馆的距离S(km)与时间t(h)的关系可以用如图的折线表示.根据图象提供的有关信息,解答下列问题: 
(1)求该团去景点时的平均速度是多少?
(2)该团在旅游景点游玩了多少小时?
(3)求返回到宾馆的时刻是几时几分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知CD⊥DA,DA⊥AB,∠1=∠2.试说明DF∥AE.请你完成下列填空,把证明过程补充完整.
证明:∵ ,
∴∠CDA=90°,∠DAB=90° ( ).
∴∠1+∠3=90°,∠2+∠4=90°.
又∵∠1=∠2,
∴ ( ),
∴DF∥AE ( ).
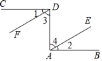
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的是用4个全等的小长方形与1个小正方形密铺而成的正方形图案.已知该图案的面积为49,小正方形的面积为4,若分别用x,y(x >y)表示小长方形的长和宽,则下列关系式中不正确的是( )

A. x+y=7 B. x-y=2 C. x2 +y2=25 D. 4xy+4=49
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,顺次连接矩形ABCD四边的中点得到四边形A1B1C1D1,然后顺次连接四边形A1B1C1D1的中点得到四边形A2B2C2D2,再顺次连接四边形A2B2C2D2四边的中点得到四边形A3B3C3D3,…,已知AB=6, BC=8,按此方法得到的四边形A5B5C5D5的周长为(______).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:(1)(-![]() )-(+
)-(+![]() )-(-
)-(-![]() )-(-
)-(-![]() );
);
(2)(-8![]() )-(+12)-(-70)-(-8
)-(+12)-(-70)-(-8![]() ); (3)(-3)-(-17)-(-33)-81.
); (3)(-3)-(-17)-(-33)-81.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com