
【题目】如图(1),已知小正方形 ABCD 的面积为1,把它的各边延长一倍得到新正方形 A 1 B 1 C 1 D 1 ;把正方形 A 1 B 1 C 1 D 1 边长按原法延长一倍得到正方形 A 2 B 2 C 2 D 2 (如图(2));以此下去,则正方形 A n B n C n D n 的面积为________.

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】把所有正偶数从小到大排列,并按如下规律分组:
第一组:2,4;
第二组:6,8,10,12;
第三组:14,16,18,20,22,24
第四组:26,28,30,32,34,36,38,40
……
则现有等式Am=(i,j)表示正偶数m是第i组第j个数(从左到右数),如A10=(2,3),则A2018=( )
A. (31,63) B. (32,17) C. (33,16) D. (34,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=30°,将△DCB绕点C顺时针旋转60°后,点D的对应点恰好与点A重合,得到△ACE,若AB=3,BC=4,则BD=(提示:可连接BE) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如下图, AB∥CD,点E,F分别为AB,CD上一点.
(1) 在AB,CD之间有一点M(点M不在线段EF上),连接ME,MF,试探究∠AEM,∠EMF,∠MFC之间有怎样的数量关系. 请补全图形,并在图形下面写出相应的数量关系,选其中一个进行证明.

(2)如下图,在AB,CD之间有两点M,N,连接ME,MN,NF,请选择一个图形写出∠AEM,∠EMN,∠MNF,∠NFC 存在的数量关系(不需证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列网格中建立平面直角坐标系如图,每个小正方形的边长均为1个单位长度.已知A(1,1)、B(3,4)和C(4,2).
(1)在图中标出点A、B、C.
(2)将点C向下平移3个单位到D点,将点A先向左平移3个单位,再向下平移1个单位到E点,在图中标出D点和E点.
(3)求△EBD的面积S△EBD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点P(1,0).点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位至点P3,第4次向右跳动3个单位至点P4,第5次又向上跳动1个单位至点P5,第6次向左跳动4个单位至点P6,…….照此规律,点P第100次跳动至点P100的坐标是( )

A. (-26,50) B. (-25,50) C. (26,50) D. (25,50)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自学:如图1,△ABC中,D是BC边上一点,则△ABD与△ADC有一个相同的高,它们的面积之比等于相应的底之比,记为 ![]() =
= ![]() .
.
(△ABD,△ADC的面积分别用记号S△ABD , S△ADC表示)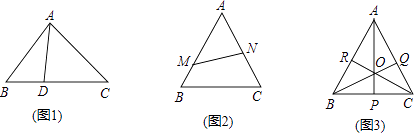
(1)心得:如图1,若BD= ![]() DC,则S△ABD:S△ADC=
DC,则S△ABD:S△ADC=
(2)成长:如图2,△ABC中,M,N分别是AB,AC边上一点,且有AM:MB=2:1,AN:NC=1:1,则△AMN与△ABC的面积比为 .
(3)巅峰:如图3,△ABC中,P,Q,R分别是BC,CA,AB边上的点,且AP,BQ,CR相交于点O,现已知△BPO,△PCO,△COQ,△AOR的面积依次为40,30,35,84,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面我们做一次折叠活动:
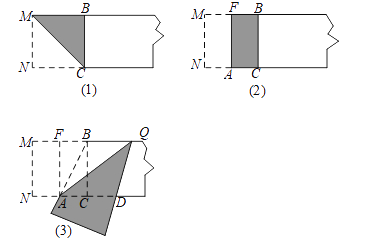
第一步,在一张宽为2的矩形纸片的一端,利用图(1)的方法折出一个正方形,然后把纸片展平,折痕为MC;
第二步,如图(2),把这个正方形折成两个相等的矩形,再把纸片展平,折痕为FA;
第三步,折出内侧矩形FACB的对角线AB,并将AB折到图(3)中所示的AD处,折痕为AQ.
根据以上的操作过程,完成下列问题:
(1)求CD的长.
(2)请判断四边形ABQD的形状,并说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com