
【题目】下面我们做一次折叠活动:
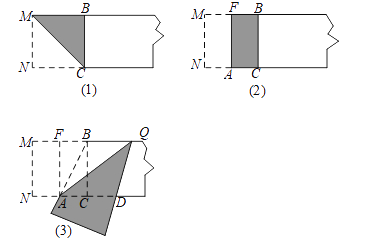
第一步,在一张宽为2的矩形纸片的一端,利用图(1)的方法折出一个正方形,然后把纸片展平,折痕为MC;
第二步,如图(2),把这个正方形折成两个相等的矩形,再把纸片展平,折痕为FA;
第三步,折出内侧矩形FACB的对角线AB,并将AB折到图(3)中所示的AD处,折痕为AQ.
根据以上的操作过程,完成下列问题:
(1)求CD的长.
(2)请判断四边形ABQD的形状,并说明你的理由.
【答案】(1)![]() ;(2)四边形ABQD是菱形.
;(2)四边形ABQD是菱形.
【解析】试题分析:(1)首先证明四边形MNCB为正方形,然后再依据折叠的性质得到:CA=1,AB=AD,最后再依据CD=AD-AC求解即可;
(2)根据平行线的性质和折叠的性质可得到∠BAQ=∠BQA,然后依据等角对等边的性质得到AB=BQ,接下来,依据一组对边平行且相等的四边形为平行四边形可证明四边形ABQD是平行四边形,再由AB=AD,可得四边形ABQD是菱形.
试题解析:(1)∵∠M=∠N=∠MBC=90°,
∴四边形MNCB是矩形,
∵MB=MN=2,
∴矩形MNCB是正方形,
∴NC=CB=2,
由折叠得:AN=AC=![]() NC=1,
NC=1,
Rt△ACB中,由勾股定理得:AB=![]() =
=![]() ,
,
∴AD=AB= ![]() ,
,
∴CD=AD﹣AC= ![]() ﹣1;
﹣1;
(2)四边形ABQD是菱形,理由是:
由折叠得:AB=AD,∠BAQ=∠QAD,
∵BQ∥AD,
∴∠BQA=∠QAD,
∴∠BAQ=∠BQA,
∴AB=BQ,
∴BQ=AD,BQ∥AD,
∴四边形ABQD是平行四边形,
∵AB=AD,
∴四边形ABQD是菱形.


科目:初中数学 来源: 题型:
【题目】如图(1),已知小正方形 ABCD 的面积为1,把它的各边延长一倍得到新正方形 A 1 B 1 C 1 D 1 ;把正方形 A 1 B 1 C 1 D 1 边长按原法延长一倍得到正方形 A 2 B 2 C 2 D 2 (如图(2));以此下去,则正方形 A n B n C n D n 的面积为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,顺次连接矩形ABCD四边的中点得到四边形A1B1C1D1,然后顺次连接四边形A1B1C1D1的中点得到四边形A2B2C2D2,再顺次连接四边形A2B2C2D2四边的中点得到四边形A3B3C3D3,…,已知AB=6, BC=8,按此方法得到的四边形A5B5C5D5的周长为(______).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,AO⊥BC,DO⊥OE.
(1)不添加其他条件情况下,请尽可能多地写出图中有关角的等量关系(至少3个);
(2)如果∠COE ![]() 350,求∠BOD的度数.
350,求∠BOD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A,B的坐标分别为(-2,3)和(1,3),抛物线y=ax2+bx+c(a<0)的顶点在线段AB上运动时,形状保持不变,且与x轴交于C,D两点(C在D的左侧),给出下列结论:①c<3;②当x<-3时,y随x的增大而增大;③若点D的横坐标最大值为5,则点C的横坐标最小值为-5;④当四边形ACDB为平行四边形时,a= ![]() .其中正确的是( )
.其中正确的是( )
A.②④
B.②③
C.①③④
D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系xOy中,点A,B分别在x轴和y轴上, ![]() =
= ![]() ,∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=
,∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y= ![]() 的图象过点C,若以CD为边的正方形的面积等于
的图象过点C,若以CD为边的正方形的面积等于 ![]() ,则k的值是.
,则k的值是.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:(1)(-![]() )-(+
)-(+![]() )-(-
)-(-![]() )-(-
)-(-![]() );
);
(2)(-8![]() )-(+12)-(-70)-(-8
)-(+12)-(-70)-(-8![]() ); (3)(-3)-(-17)-(-33)-81.
); (3)(-3)-(-17)-(-33)-81.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中以点A为圆心,AB为半径作圆A交网格于点C(如图(1)),过点C作圆的切线交网格于点D,以点A为圆心,AD为半径作圆交网格于点E(如图(2)). 问题:
(1)求∠ABC的度数;
(2)求证:△AEB≌△ADC;
(3)△AEB可以看作是由△ADC经过怎样的变换得到的?并判断△AED的形状(不用说明理由).
(4)如图(3),已知直线a,b,c,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形A′B′C′,使三个顶点A′,B′,C′,分别在直线a,b,c上.要求写出简要的画图过程,不需要说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com