
【题目】如图所示的是用4个全等的小长方形与1个小正方形密铺而成的正方形图案.已知该图案的面积为49,小正方形的面积为4,若分别用x,y(x >y)表示小长方形的长和宽,则下列关系式中不正确的是( )

A. x+y=7 B. x-y=2 C. x2 +y2=25 D. 4xy+4=49
【答案】C
【解析】
观察图形发现,x+y表示大正方形的边长,x-y表示小正方形的边长,4xy+4表示大正方形的面积,进而联系所求得的两个正方形的边长,结合已知图案的总面积,即可求解.
∵大正方形的面积为49,小正方形的面积为4,
∴大正方形的边长为7,小正方形的边长为2.
∵x+y表示大正方形的边长,
∴x+y=7,故A正确;
∵x-y表示小正方形的边长,
∴x-y=2,故B正确;
∵x2+y2=(x-y)2+2xy,
∴x2+y2表示小正方形与两个小矩形的面积之和,
∴x2+y2=(49-4)÷4×2+4=26.5≠25,故C错误;
∵4xy+4表示大正方形的面积,
∴4xy+4=49,故D正确.
故选C.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】用简便方法计算:
(1)(-3![]() )+(+8
)+(+8![]() )-(-5
)-(-5![]() );
);
(2)(-![]() )+(+
)+(+![]() )+(+
)+(+![]() )+(-1
)+(-1![]() );
);
(3)(-3![]() )-(-
)-(-![]() )+(-0.5)+3
)+(-0.5)+3![]() ;
;
(4)(+3![]() )+(-2
)+(-2![]() )-(-5
)-(-5![]() )-(+
)-(+![]() );
);
(5)(-0.25)+(-3)-|-1![]() |-(-3);
|-(-3);
(6)(+![]() )+(+17)+(-1
)+(+17)+(-1![]() )-(+7)-(-2
)-(+7)-(-2![]() )+(-
)+(-![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列网格中建立平面直角坐标系如图,每个小正方形的边长均为1个单位长度.已知A(1,1)、B(3,4)和C(4,2).
(1)在图中标出点A、B、C.
(2)将点C向下平移3个单位到D点,将点A先向左平移3个单位,再向下平移1个单位到E点,在图中标出D点和E点.
(3)求△EBD的面积S△EBD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次期中考试中,
(1)一个班级有甲、乙、丙三名学生,分别得到70分、80分、90分.这三名同学的平均得分是多少?
(2)一个班级共有40名学生,其中5人得到70分,20人得到80分,15人得到90分.求班级的平均得分.
(3)一个班级中,20%的学生得到70分,50%的学生得到80分,30%的学生得到90分.求班级的平均得分.
(4)中考的各学科的分值依次为:数学150分,语文150分,物理100分,政治50分,历史50分,合计总分为500分. 在这次期中考试中,各门学科的总分都设置为100分,现已知甲、乙两名学生的得分如下表:
学科 | 数学 | 语文 | 物理 | 政治 | 历史 |
甲 | 80 | 90 | 80 | 80 | 70 |
乙 | 80 | 80 | 70 | 80 | 95 |
你认为哪名同学的成绩更理想,写出你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自学:如图1,△ABC中,D是BC边上一点,则△ABD与△ADC有一个相同的高,它们的面积之比等于相应的底之比,记为 ![]() =
= ![]() .
.
(△ABD,△ADC的面积分别用记号S△ABD , S△ADC表示)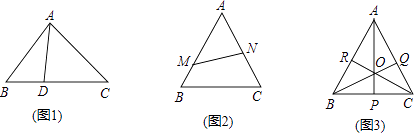
(1)心得:如图1,若BD= ![]() DC,则S△ABD:S△ADC=
DC,则S△ABD:S△ADC=
(2)成长:如图2,△ABC中,M,N分别是AB,AC边上一点,且有AM:MB=2:1,AN:NC=1:1,则△AMN与△ABC的面积比为 .
(3)巅峰:如图3,△ABC中,P,Q,R分别是BC,CA,AB边上的点,且AP,BQ,CR相交于点O,现已知△BPO,△PCO,△COQ,△AOR的面积依次为40,30,35,84,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】6月5日是“世界环境日”,某校从3名男生和2名女生中随机抽取学生去参加市中学生环保演讲比赛.
(1)若抽取1名学生参加,恰好是男生的概率是;
(2)如果抽取1名学生参加,请用列表或树状图求出恰好是1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明有5张写着不同的数字的卡片,请你按要求抽出卡片,完成下列各问题:
![]()
(1)从中取出2张卡片,使这2张卡片上数字乘积最大,最大值是 ;
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,最小值是 ;
(3)从中取出4张卡片,用学过的运算方法,使结果为24.写出运算式子:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com