Question

【题目】如图，在直角坐标系中， B（0，8），D（10，0），一次函数y=x+的图象过C（16，n），与x轴交于A点。

（1）求证：四边形ABCD为平行四边形；

（2）将△AOB绕点O顺时针旋转，旋转得△A1OB1，问：能否使以点O、A1、D、B1为顶点的四边形是平行四边形？若能，求点A1的坐标；若不能，请说明理由；

Answer 1

【答案】（1）见解析；（2）能，所求满足条件的A1为：（―， ）、（， ）、（，―）

【解析】整体分析：

（1）把点过C（16，n）代入到y=x+，求出n，得到点C的坐标，求出点A的坐标，由AD与BC平行且相等证明；（2）分三种情况讨论，有两种是A1B1与OD平行，一种是A1B1与OD相交，结合平行四边形的性质和勾股定理求解.

解：（1）∵y=x+的图象过C（16，n），A两点，∴n=×16+=8，

∴C（16，8），A（－6，0）.

∵B（0，8），∴BD∥x轴，

又∵AD=10―（―6）=16=BC，

∴四边形ABCD为平行四边形

（2）由题意可知；AB=A1B1=10，∠AOB=∠A1OB1=90°

①△AOB旋转后，若A1B1∥x轴，构成四边形OA1B1D如图①,

又∵A1B1=OD=10，∴四边形OA1B1D构成平行四边形，

此时，设A1B1与y轴交于H，

则OH==，A1H==，

∴A1（―， ）.

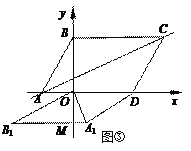
②△AOB旋转后，若A1B1的中点E在x轴上，构成四边形OA1DB1如图②.

∵∠A1OB1=90°，∴OE=A1B1=5，∴OE=ED=5，

∴四边形OA1DB1构成平行四边形，

设作A1N⊥x轴交于N，∠A1OB1=∠OA1D=90°.

则AN==，ON==，

∴A1（， ）.

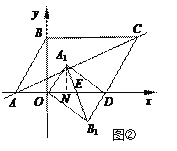
③△AOB旋转后，若A1B1∥x轴，构成四边形ODA1B1如图③，

又∵A1B1=OD=10，∴四边形ODA1B1构成平行四边形，

此时，设A1B1与y轴交于M，

则OM==，A1M==，

∴A1（，―）.

综上所述，所求满足条件的A1为（―， ）、（， ）、（，―）