
【题目】“摩拜单车”公司调查无锡市民对其产品的了解情况,随机抽取部分市民进行问卷,结果分“非常了解”、“比较了解”、“一般了解”、“不了解”四种类型,分别记为![]() 、
、![]() 、
、![]() 、
、![]() .根据调查结果绘制了如下尚不完整的统计图.
.根据调查结果绘制了如下尚不完整的统计图.

(1)本次问卷共随机调查了 名市民,扇形统计图中![]() .
.
(2)请根据数据信息补全条形统计图.
(3)扇形统计图中“D类型”所对应的圆心角的度数是 .
(4)从这次接受调查的市民中随机抽查一个,恰好是“不了解”的概率是 。
科目:初中数学 来源: 题型:
【题目】如图1,在8×8方格纸中,△ABC的三个顶点都在小方格的顶点上,按要求画一个三角形,使它的顶点都在方格的顶点上.请在图2中画一个三角形,使它与△ABC相似,且相似比为2:1;请在图3中画一个三角形,使它与△ABC相似,且相似比为 ![]() :1.
:1. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)﹣![]() a2bc+
a2bc+![]() cba2
cba2
(2)7ab﹣3a2b2+7+8ab2+3a2b2﹣3﹣7ab
(3)(﹣x+2x2+5)+(4x2﹣3﹣6x)
(4)(2x2﹣![]() +3x)﹣4(x﹣x2+
+3x)﹣4(x﹣x2+![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
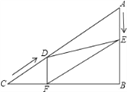
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P(2a﹣12,1﹣a)位于第三象限,点Q(x,y)位于第二象限且是由点P向上平移一定单位长度得到的.
(1)若点P的纵坐标为﹣3,试求出a的值;
(2)在(1)题的条件下,试求出符合条件的一个点Q的坐标;
(3)若点P的横、纵坐标都是整数,试求出a的值以及线段PQ长度的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中, B(0,8),D(10,0),一次函数y=![]() x+
x+![]() 的图象过C(16,n),与x轴交于A点。
的图象过C(16,n),与x轴交于A点。
(1)求证:四边形ABCD为平行四边形;
(2)将△AOB绕点O顺时针旋转,旋转得△A1OB1,问:能否使以点O、A1、D、B1为顶点的四边形是平行四边形?若能,求点A1的坐标;若不能,请说明理由;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的顶点A、C在双曲线y1=﹣ ![]() 上,B、D在双曲线y2=
上,B、D在双曲线y2= ![]() 上,k1=2k2(k1>0),AB∥y轴,SABCD=24,则k1= .
上,k1=2k2(k1>0),AB∥y轴,SABCD=24,则k1= . 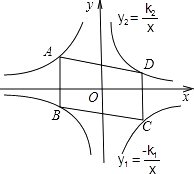
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是安装在斜屋面上的热水器,图2是安装该热水器的侧面示意图.已知,斜屋面的倾角为25°,长为2.1米的真空管AB与水平线AD的夹角为40°,安装热水器的铁架水平横管BC长0.2米,求铁架垂直管CE的长(结果精确到0.01米). 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com