
【题目】如图所示,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
【答案】(1)详见解析;(2)当t=10时,AEFD是菱形;(3)当t=![]() 时△DEF是直角三角形(∠EDF=90°);
时△DEF是直角三角形(∠EDF=90°);
当t=![]() 时,△DEF是直角三角形(∠DEF=90°),理由见解析.
时,△DEF是直角三角形(∠DEF=90°),理由见解析.
【解析】试题分析:(1)利用t表示出CD以及AE的长,然后在直角△CDF中,利用直角三角形的性质求得DF的长,即可证明;
(2)易证四边形AEFD是平行四边形,当AD=AE时,四边形AEFD是菱形,据此即可列方程求得t的值;
(3)分两种情况讨论即可求解.
【解答】(1)证明:∵直角△ABC中,∠C=90°﹣∠A=30°.
∵CD=4t,AE=2t,
又∵在直角△CDF中,∠C=30°,
∴DF=CD=2t,
∴DF=AE;
解:(2)∵DF∥AB,DF=AE,
∴四边形AEFD是平行四边形,
当AD=AE时,四边形AEFD是菱形,
即60﹣4t=2t,
解得:t=10,
即当t=10时,AEFD是菱形;
(3)当t=![]() 时△DEF是直角三角形(∠EDF=90°);
时△DEF是直角三角形(∠EDF=90°);
当t=12时,△DEF是直角三角形(∠DEF=90°).理由如下:
当∠EDF=90°时,DE∥BC.
∴∠ADE=∠C=30°
∴AD=2AE
∵CD=4t,
∴DF=2t=AE,
∴AD=4t,
∴4t+4t=60,
∴t=![]() 时,∠EDF=90°.
时,∠EDF=90°.
当∠DEF=90°时,DE⊥EF,
∵四边形AEFD是平行四边形,
∴AD∥EF,
∴DE⊥AD,
∴△ADE是直角三角形,∠ADE=90°,
∵∠A=60°,
∴∠DEA=30°,
∴AD=AE,
AD=AC﹣CD=60﹣4t,AE=DF=CD=2t,
∴60﹣4t=t,
解得t=12.
综上所述,当t=![]() 时△DEF是直角三角形(∠EDF=90°);当t=12时,△DEF是直角三角形(∠DEF=90°).
时△DEF是直角三角形(∠EDF=90°);当t=12时,△DEF是直角三角形(∠DEF=90°).


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
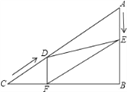
【题目】已知,正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N,AH⊥MN于点H.
(1)如图①,当∠MAN绕点A旋转到BM=DN时,请你直接写出AH与AB的数量关系: ;
(2)如图②,当∠MAN绕点A旋转到BM≠DN时,(1)中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明;
(3)如图③,已知∠MAN=45°,AH⊥MN于点H,且MH=2,NH=3,求AH的长.(可利用(2)得到的结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在以点O为原点的直角坐标系中,一次函数y=-![]() x+1的图象与x轴交于A,与y轴交于点B,点C在第二象限内且为直线AB上一点,OC=
x+1的图象与x轴交于A,与y轴交于点B,点C在第二象限内且为直线AB上一点,OC=![]() AB,反比例函数y=
AB,反比例函数y=![]() 的图象经过点C,则k的值为 .
的图象经过点C,则k的值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数乘方的符号法则:
(1)正数的任何次幂都是________;
(2)负数的奇次幂是________,负数的偶次幂是________;
(3)0的任何正整数次幂都是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题的个数为( )
①同位角相等;②从直线外一点到这条直线的垂线段,叫作这点到直线的距离;③平面内经过一点有且只有一条直线与已知直线平行;④平面内不相交的两条直线叫作平行线.
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
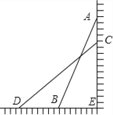
【题目】如图,将长为2.5米长的梯子AB斜靠在墙上,此时BE的长为0.7米.
(1)求梯子上端到墙的底端E的距离(即AE的长);
(2)如果梯子的顶端A沿墙下滑0.4米(即AC=0.4米),则梯脚B将外移(即BD长)多少米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com