
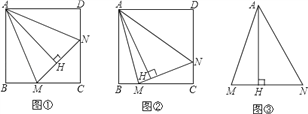
【题目】已知,正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N,AH⊥MN于点H.
(1)如图①,当∠MAN绕点A旋转到BM=DN时,请你直接写出AH与AB的数量关系: ;
(2)如图②,当∠MAN绕点A旋转到BM≠DN时,(1)中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明;
(3)如图③,已知∠MAN=45°,AH⊥MN于点H,且MH=2,NH=3,求AH的长.(可利用(2)得到的结论)
【答案】(1)AH=AB;(2)数量关系成立,证明见试题解析;(3)6.
【解析】试题分析:(1)由三角形全等可以证明AH=AB;
(2)延长CB至E,使BE=DN,证明△AEM≌△ANM,能得到AH=AB;
(3)分别沿AM、AN翻折△AMH和△ANH,得到△ABM和△AND,然后分别延长BM和DN交于点C,得正方形ABCE,设AH=x,则MC=x﹣2,NC=x﹣3,在Rt△MCN中,由勾股定理,解得x.
试题解析:(1)如图①AH=AB.
(2)数量关系成立.如图②,延长CB至E,使BE=DN.
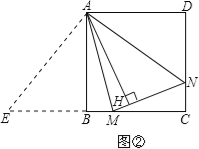
∵ABCD是正方形,∴AB=AD,∠D=∠ABE=90°,在Rt△AEB和Rt△AND中, ,∴Rt△AEB≌Rt△AND,∴AE=AN,∠EAB=∠NAD,∴∠EAM=∠NAM=45°,在△AEM和△ANM中,
,∴Rt△AEB≌Rt△AND,∴AE=AN,∠EAB=∠NAD,∴∠EAM=∠NAM=45°,在△AEM和△ANM中,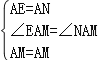 ,∴△AEM≌△ANM.∵AB、AH是△AEM和△ANM对应边上的高,∴AB=AH.
,∴△AEM≌△ANM.∵AB、AH是△AEM和△ANM对应边上的高,∴AB=AH.
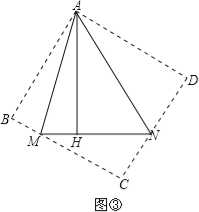
(3)如图③分别沿AM、AN翻折△AMH和△ANH,得到△ABM和△AND,∴BM=2,DN=3,∠B=∠D=∠BAD=90°.分别延长BM和DN交于点C,得正方形ABCD,由(2)可知,AH=AB=BC=CD=AD.设AH=x,则MC=x﹣2,NC=x﹣3,在Rt△MCN中,由勾股定理,得MN2=MC2+NC2,∴![]() ,
,
解得![]() ,
,![]() (不符合题意,舍去).∴AH=6.
(不符合题意,舍去).∴AH=6.


科目:初中数学 来源: 题型:
【题目】如图,已知点A(1,a)是反比例函数![]() 的图象上一点,直线
的图象上一点,直线![]() 与反比例函数
与反比例函数![]() 的图象在第四象限的交点为点B.
的图象在第四象限的交点为点B.
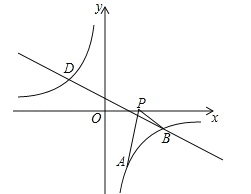
(1)求直线AB的解析式;
(2)动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中,是必然事件的是( )
A. 380人中有两个人的生日在同一天 B. 两条线段可以组成一个三角形
C. 打开电视机,它正在播放新闻联播 D. 三角形的内角和等于360°
查看答案和解析>>
科目:初中数学 来源: 题型:
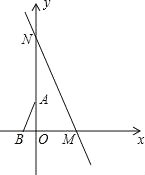
【题目】如图,在直角坐标系中,直线y=-![]() 分别与x轴、y轴交于点M、N,点A、B分别在y轴、x轴上,且∠B=60°,AB=2,将△ABO绕原点O顺时针转动一周,当AB与直线MN平行时点A的坐标为 .
分别与x轴、y轴交于点M、N,点A、B分别在y轴、x轴上,且∠B=60°,AB=2,将△ABO绕原点O顺时针转动一周,当AB与直线MN平行时点A的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
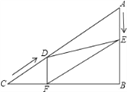
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com