Question

【题目】如图①，在正方形ABCD中，对角线AC、BD交于点O，动点P在线段BC上（不含点B），∠BPE= ∠ACB，PE交BO于点E，过点B作BF⊥PE，垂足为F，交AC于点G．

（1）如图②，当点P与点C重合时，求证：△BOG≌△POE；
（2）通过观察、测量、猜想： = ， 并结合图①证明你的猜想；
（3）把正方形ABCD改为菱形，其他条件不变（如图②），若∠ACB=a，直接写出 的值，为 ． （用含a的式子表示）

Answer 1

【答案】
（1）

证明：∵四边形ABCD是正方形，P与C重合，

∴OB=OP，∠BOC=∠BOG=90°，

∵PF⊥BG，∠PFB=90°，

∴∠GBO=90°﹣∠BGO，∠EPO=90°﹣∠BGO，

∴∠GBO=∠EPO，

在△BOG和△POE中， ，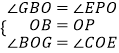

∴△BOG≌△POE（ASA）

（2）
（3）tanα
【解析】（2.）解：猜想 = ．
证明：如图2，过P作PM∥AC交BG于M，交BO于N，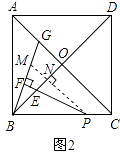

∴∠PNE=∠BOC=90°，∠BPN=∠OCB．
∵∠OBC=∠OCB=45°，
∴∠NBP=∠NPB．
∴NB=NP．
∵∠MBN=90°﹣∠BMN，∠NPE=90°﹣∠BMN，
∴∠MBN=∠NPE，
在△BMN和△PEN中， ，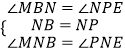
∴△BMN≌△PEN（ASA），
∴BM=PE．
∵∠BPE= ∠ACB，∠BPN=∠ACB，
∴∠BPF=∠MPF．
∵PF⊥BM，
∴∠BFP=∠MFP=90°．
在△BPF和△MPF中， ，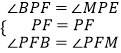
∴△BPF≌△MPF（ASA）．
∴BF=MF．
即BF= BM．
∴BF= PE．
即 = ；
故答案为 ；
（3.）解：如图3，过P作PM∥AC交BG于点M，交BO于点N，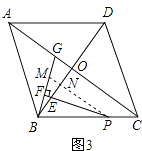

∴∠BPN=∠ACB=α，∠PNE=∠BOC=90°．
由（2）同理可得BF= BM，∠MBN=∠EPN，
∴△BMN∽△PEN，
∴ = ．
在Rt△BNP中，tanα= ，
∴ =tanα．即 =tanα．
∴ =tanα．
（1）由四边形ABCD是正方形，P与C重合，易证得OB=OP，∠BOC=∠BOG=90°，由同角的余角相等，证得∠GBO=∠EPO，则可利用ASA证得：△BOG≌△POE；（2）首先过P作PM∥AC交BG于M，交BO于N，易证得△BMN≌△PEN（ASA），△BPF≌△MPF（ASA），即可得BM=PE，BF= BM．则可求得 的值；（3）首先过P作PM∥AC交BG于点M，交BO于点N，由（2）同理可得：BF= BM，∠MBN=∠EPN，继而可证得：△BMN∽△PEN，然后由相似三角形的对应边成比例，求得 ．