
����Ŀ���±����������ƶ��绰�Ʒѷ�ʽ��
��ʹ�÷�(Ԫ) | ������ʱ��(����) | ���г�ʱ��(Ԫ/����) | ���� | |
��ʽһ | 65 | 160 | 0.25 | ��� |
��ʽ�� | 100 | 380 | 0.19 | ��� |
˵������ʹ�÷ѹ̶���ȡ�����в�����ʱ�䲻���շѣ����г�ʱ���ּ��ճ�ʱ�ѣ�������ѣ�
(1)�����ij������ͨ��ʱ��Ϊ200������������ʽһ�Ʒ����� ��Ԫ������ʽ���Ʒ����� ��Ԫ����������ʽ���Ʒ���103.8Ԫ��������ͨ��ʱ��Ϊ�� �����ӣ�
(2)�Ƿ����ij����ͨ��ʱ��t(����)������ʽһ�ͷ�ʽ���ļƷ���ȣ������ڣ������t��ֵ���������ڣ���˵�����ɣ�
(3)����ͨ�����������ֱ�Ӹ�����������ͨ��ʱ��t(����)����ʲô����ʱ��ѡ��ʽһʡǮ����ÿ������ͨ��ʱ��t(����)����ʲô����ʱ��ѡ��ʽ��ʡǮ��
���𰸡�(1)75��100��400��(2)��t��300ʱ����ʽһ�ͷ�ʽ���ļƷ���ȣ�(3)��������ͨ��ʱ��С��300����ʱ��ѡ��Ʒѷ�ʽһʡǮ����������ͨ��ʱ�����300����ʱ��ѡ�����ּƷѷ�ʽ������ȣ���������ͨ��ʱ�����300����ʱ��ѡ��Ʒѷ�ʽ��ʡǮ��
��������
��1���������ּƷѷ�ʽ�շѱ���ʽ���㣬����������ۣ�
��2����t��160��160��t��380��t��380����������ǣ��ٵ�t��160ʱ����65��100�ɵó������ڼƷ���ȣ��ڵ�160��t��380ʱ���ɼƷ���ȣ����ɵó�����t��һԪһ�η��̣���֮���ɵó����ۣ��۵�t��380ʱ���ɼƷ���ȣ����ɵó�����t��һԪһ�η��̣���֮���ɵó�tֵ���ɸ�tֵ������380�ɵó������ڼƷ���ȣ����ϼ��ɵó����ۣ�
��3����t��160��160��t��300��t��300��300��t��380��t��380��������Ƚ����ּƷѷ�ʽ�շѵĶ��٣�����ý⣮
(1)����ʽһ�Ʒ��裺65+(200��160)��0.25��75(Ԫ)��
����ʽ���Ʒ���100Ԫ��
����ͨ��ʱ��(103.8��100)��0.19+380��400(����)��
�ʴ�Ϊ��75��100��400��
(2)�ٵ�t��160ʱ����ʽһ�Ʒ���65Ԫ����ʽ���Ʒ���100Ԫ��
����ڼƷ���ȣ�
�ڵ�160��t��380ʱ����65+0.25(t��160)��100��
��ã�t��300��
�۵�t��380ʱ����65+0.25(t��160)��100+0.19(t��380)��
��ã�t��![]() ��
��
��![]() ��380��
��380��
����ȥ���������ڼƷ���ȣ�
������������t��300ʱ����ʽһ�ͷ�ʽ���ļƷ���ȣ�
(3)��0��t��160ʱ��75��100��
��ѡ�Ʒѷ�ʽһʡǮ��
��160��t��300ʱ��65+0.25(t��160)��100��
��ѡ�Ʒѷ�ʽһʡǮ��
��t��300ʱ��65+0.25(t��160)��100��
�����ּƷѷ�ʽ������ȣ�
��300��t��380ʱ��65+0.25(t��160)��100��
��ѡ�Ʒѷ�ʽ��ʡǮ��
��t��380ʱ��65+0.25(t��160)��100+0.19(t��380)��
��ѡ�Ʒѷ�ʽ��ʡǮ��
������������������ͨ��ʱ��С��300����ʱ��ѡ��Ʒѷ�ʽһʡǮ����������ͨ��ʱ�����300����ʱ��ѡ�����ּƷѷ�ʽ������ȣ���������ͨ��ʱ�����300����ʱ��ѡ��Ʒѷ�ʽ��ʡǮ��
�ʴ�Ϊ��(1)75��100��400��(2)��t��300ʱ����ʽһ�ͷ�ʽ���ļƷ���ȣ�(3)��������ͨ��ʱ��С��300����ʱ��ѡ��Ʒѷ�ʽһʡǮ����������ͨ��ʱ�����300����ʱ��ѡ�����ּƷѷ�ʽ������ȣ���������ͨ��ʱ�����300����ʱ��ѡ��Ʒѷ�ʽ��ʡǮ��


 ������ҵ��ͬ����ϰ��ϵ�д�
������ҵ��ͬ����ϰ��ϵ�д� С��ſ�ʱ��ҵϵ�д�
С��ſ�ʱ��ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����5��5�������������У����ڸ���ϵĵ�A��B��C��D����ȡ���㣬�����ɵ�������ǡ����ֱ�������εĸ���Ϊ�� ��
A.1
B.2
C.3
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC���CDE���ǵȱ������Σ���B��C��D��ͬһֱ���ϣ�AD��BE�ཻ�ڵ�G��BE��AC�ཻ�ڵ�F��AD��CE�ཻ�ڵ�H�������н��ۣ��١�ACD�ա�BCE���ڡ�AGB=60�㣻��BF=AH���ܡ�CFH�ǵȱ������Σ�����CG�����BGC=��DGC ����EG+GC=GD. ������ȷ����________.��ֻҪд��ţ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��0��4����C����2��0����ֱ��l��y��kx+b�ϣ�l�ͺ���y����4x+a��ͼ���ڵ�B
��1����ֱ��l�ı���ʽ��
��2������B�ĺ�������1�������x��y�ķ�����![]() �Ľ⼰a��ֵ��
�Ľ⼰a��ֵ��
��3������A����x��ĶԳƵ�ΪP�����PBC�������
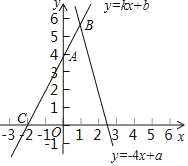
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
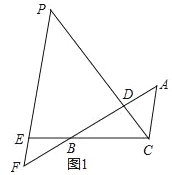
����Ŀ����ͼ1����ABC�У���D���߶�AB�ϣ���E���߶�CB�ӳ����ϣ���BE=CD��EP��AC��ֱ��CD�ڵ�P����ֱ��AB�ڵ�F����ADP=��ACB��
��1��ͼ1���Ƿ������AC��ȵ��߶Σ������ڣ����ҳ���������֤�����������ڣ�˵�����ɣ�
��2����������D���߶�AB�ϣ���E���߶�CB�ӳ���������Ϊ����D���߶�BA�ӳ����ϣ���E���߶�BC�ӳ��������������������䣨��ͼ2��������ABC=90�㣬��BAC=60�㣬AB=2ʱ�����߶�PE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ȼ�������ֵ:��a=9ʱ����a+![]() ��ֵ���������˵Ľ������:
��ֵ���������˵Ľ������:
�Ľ��Ϊ:ԭʽ=a+![]() =a+(1-a)=1.
=a+(1-a)=1.
�ҵĽ��Ϊ:ԭʽ=a+![]() =a+(a-1)=2a-1=17.
=a+(a-1)=2a-1=17.
���ֽ���У�_____�Ľ���Ǵ����,�����ԭ���ǵ�a=9ʱ______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1�dz�����ֽ������ֽ����EF�۵���ͼ2������BF�۵���ͼ3.
��1������DEF=20������ͼ3�С�CFE�����Ƕ��٣�
��2������DEF=a����ͼ3�С�CFE��a��ʾ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
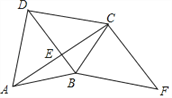
����Ŀ����ͼ���ı���ABCD�ĶԽ���AC��BD�ڵ�E��AB=BC��FΪ�ı���ABCD��һ�㣬�ҡ�FCA=90������CBF=��DCB��
��1����֤���ı���DBFC��ƽ���ı��Σ�
��2�����BCƽ�֡�DBF����CDB=45����BD=2����AC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͨ������ɲ�����ֻ��еľ��������㳵����ʻ���ٶȣ����õľ��鹫ʽ��u=16![]() ������u��ʾ���٣���λ��km/h����d��ʾɲ�����루��λ��m����f��ʾĦ��ϵ������һ�ν�ͨ�¹��У����d=20m��f=1.44����������ͨ�¹ʵ�·������Ϊ80km/h�����������Ƿ�Υ�泬����ʻ��˵�����ɣ����ο����ݣ�
������u��ʾ���٣���λ��km/h����d��ʾɲ�����루��λ��m����f��ʾĦ��ϵ������һ�ν�ͨ�¹��У����d=20m��f=1.44����������ͨ�¹ʵ�·������Ϊ80km/h�����������Ƿ�Υ�泬����ʻ��˵�����ɣ����ο����ݣ�![]() ��1.4��
��1.4��![]() ��2.2��
��2.2��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com