
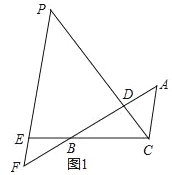
【题目】如图1,△ABC中,点D在线段AB上,点E在线段CB延长线上,且BE=CD,EP∥AC交直线CD于点P,交直线AB于点F,∠ADP=∠ACB.
(1)图1中是否存在与AC相等的线段?若存在,请找出,并加以证明,若不存在,说明理由;
(2)若将“点D在线段AB上,点E在线段CB延长线上”改为“点D在线段BA延长线上,点E在线段BC延长线上”,其他条件不变(如图2).当∠ABC=90°,∠BAC=60°,AB=2时,求线段PE的长.

【答案】(1)见解析;(2)6
【解析】(1)先证△CBD∽△ABC,再转化比例线段即可得出答案;
(2)利用平行线的性质、30度角所对的直角边等于斜边的一半、三角形中位线定理即可得出答案.
解:(1)AC=BF.证明如下:
如图1,∵∠ADP=∠ACD+∠A,∠ACB=∠ACD+∠BCD,∠ADP=∠ACB,
∴∠BCD=∠A,
又∵∠CBD=∠ABC,
∴△CBD∽△ABC,
∴![]() ,①
,①
∵FE∥AC,
∴![]() ,②
,②
由①②可得, ![]() ,
,
∵BE=CD,
∴BF=AC;
(2)如图2,∵∠ABC=90°,∠BAC=60°,
∴∠ACB=30°=∠ADP,
∴∠BCD=60°,∠ACD=60°﹣30°=30°,
∵PE∥AC,
∴∠E=∠ACB=30°,∠CPE=∠ACD=30°,
∴CP=CE,
∵BE=CD,
∴BC=DP,
∵∠ABC=90°,∠D=30°,
∴BC=![]() CD,
CD,
∴DP=![]() CD,即P为CD的中点,
CD,即P为CD的中点,
又∵PF∥AC,
∴F是AD的中点,
∴FP是△ADC的中位线,
∴FP=![]() AC,
AC,
∵∠ABC=90°,∠ACB=30°,
∴AB=![]() AC,
AC,
∴FP=AB=2,
∵DP=CP=BC,CP=CE,
∴BC=CE,即C为BE的中点,
又∵EF∥AC,
∴A为FB的中点,
∴AC是△BEF的中位线,
∴EF=2AC=4AB=8,
∴PE=EF﹣FP=8﹣2=6.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点P从点A出发,沿着正方形的边顺时针方向运动一周,则△APC的面积y与点P运动的路程x之间形成的函数关系图象大致是( )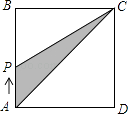
A.
B.
C.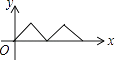
D.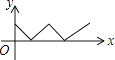
查看答案和解析>>
科目:初中数学 来源: 题型:
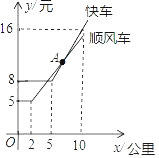
【题目】如图表示某公司“顺风车”与“快车”的行驶里程x(千米)与计费y(元)之间的函数图象.
(1)由图象写出乘车里程为5千米时选择 (“顺风车”或“快车”)更便宜;
(2)当x>5时,顺风车的函数是y=![]() x+
x+![]() ,判断乘车,里程是8千米时,选择“顺风车”和“快车”哪个更便宜?说明理由.
,判断乘车,里程是8千米时,选择“顺风车”和“快车”哪个更便宜?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=x3﹣3x的图象如图所示,则以下关于该函数图象及其性质的描述正确的是( ) 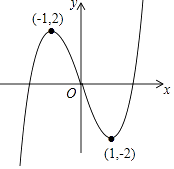
A.函数最大值为2
B.函数图象最低点为(1,﹣2)
C.函数图象关于原点对称
D.函数图象关于y轴对称
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表中有两种移动电话计费方式:
月使用费(元) | 主叫限定时间(分钟) | 主叫超时费(元/分钟) | 被叫 | |
方式一 | 65 | 160 | 0.25 | 免费 |
方式二 | 100 | 380 | 0.19 | 免费 |
说明:月使用费固定收取,主叫不超限定时间不再收费,主叫超时部分加收超时费;被叫免费.
(1)若李杰某月主叫通话时间为200分钟则他按方式一计费需 元,按方式二计费需 元;若他按方式二计费需103.8元,则主叫通话时间为 分钟;
(2)是否存在某主叫通话时间t(分钟),按方式一和方式二的计费相等,若存在,请求出t的值;若不存在,请说明理由;
(3)请你通过计算分析后,直接给出当月主叫通话时间t(分钟)满足什么条件时,选择方式一省钱;当每月主叫通话时间t(分钟)满足什么条件时,选择方式二省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着智能手机的普及,微信抢红包已成为春节期间人们最喜欢的活动之一,某校七年级(1)班班长对全班50名学生在春节期间所抢的红包金额进行统计,并绘制成了统计图.
请根据以上信息回答: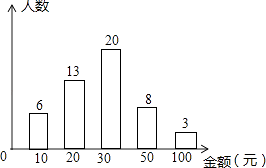
(1)该班同学所抢红包金额的众数是 , 中位数是;
(2)该班同学所抢红包的平均金额是多少元?
(3)若该校共有18个班级,平均每班50人,请你估计该校学生春节期间所抢的红包总金额为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形OABC的边OA在x轴上,AC与OB交于点D (8,4),反比例函数y= ![]() 的图象经过点D.若将菱形OABC向左平移n个单位,使点C落在该反比例函数图象上,则n的值为 .
的图象经过点D.若将菱形OABC向左平移n个单位,使点C落在该反比例函数图象上,则n的值为 . 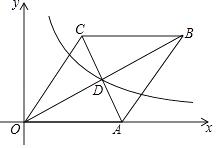
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,(1)∵∠A=_____(已知),
∴AC∥ED( )
(2)∵∠2=_____(已知),
∴AC∥ED( )
(3)∵∠A+_____=180°(已知),
∴AB∥FD( )
(4)∵AB∥_____(已知),
∴∠2+∠AED=180°( )
(5)∵AC∥_____(已知),
∴∠C=∠1( )
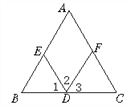
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com