【题目】函数y=x3﹣3x的图象如图所示，则以下关于该函数图象及其性质的描述正确的是（ ）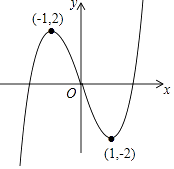 
A.函数最大值为2
B.函数图象最低点为（1，﹣2）
C.函数图象关于原点对称
D.函数图象关于y轴对称
科目：初中数学 来源： 题型：
【题目】填表：
相反数等于它本身 | 绝对值等于它本身 | 倒数等于它本身 | 平方等于它本身 | 立方等于它本身 | 平方根等于它本身 | 算术平方根等于它本身 | 立方根等于它本身 | 最大的负整数 | 绝对值最小的数 |
查看答案和解析>>
科目：初中数学 来源： 题型：
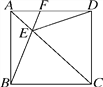
【题目】在正方形ABCD中，AC为对角线，点E为AC上一点，连接EB，ED.
(1)求证：△BEC≌△DEC；
(2)延长BE交AD于点F，当∠BED＝120°时，求∠EFD的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点B、E分别在直线AC和DF上，若∠AGB＝∠EHF，∠C＝∠D，可以证明
∠A＝∠F．请完成下面证明过程中的各项“填空”
证明：∵∠AGB＝∠EHF（已知）
∠AGB＝ （对顶角相等）
∴∠EHF＝∠DGF（等量代换）
∴ ∥EC（理由： ）
∴∠ ＝∠DBA（两直线平行，同位角相等）
又∵∠C＝∠D，∴∠DBA＝ （等量代换）
∴DF∥ （内错角相等，两直线平行）
∴∠A＝∠F（理由： ）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，⊙O是Rt△ABC的外接圆，∠ABC=90°，弦BD=BA，AB=12，BC=5，BE⊥DC交DC的延长线于点E． 
（1）求证：∠BCA=∠BAD；
（2）求DE的长；
（3）求证：BE是⊙O的切线．
查看答案和解析>>
科目：初中数学 来源： 题型：
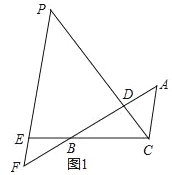
【题目】如图1，△ABC中，点D在线段AB上，点E在线段CB延长线上，且BE=CD，EP∥AC交直线CD于点P，交直线AB于点F，∠ADP=∠ACB．
（1）图1中是否存在与AC相等的线段？若存在，请找出，并加以证明，若不存在，说明理由；
（2）若将“点D在线段AB上，点E在线段CB延长线上”改为“点D在线段BA延长线上，点E在线段BC延长线上”，其他条件不变（如图2）．当∠ABC=90°，∠BAC=60°，AB=2时，求线段PE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC，点D，E分别在边BC 和AC上，若AD=AE，则下列结论错误的是（ ）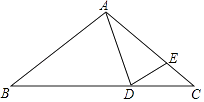 
A.∠ADB=∠ACB+∠CAD
B.∠ADE=∠AED
C.∠CDE= 
∠BAD
D.∠AED=2∠ECD
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠BAC=90°，AB=4，AC=6，点D、E分别是BC．AD的中点，AF∥BC交CE的延长线于F．则四边形AFBD的面积为______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在ABCD中，∠ABC的平分线交AD于点E，延长BE交CD的延长线于F．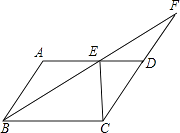 
（1）若∠F=20°，求∠A的度数；
（2）若AB=5，BC=8，CE⊥AD，求ABCD的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
