
【题目】如图表示某公司“顺风车”与“快车”的行驶里程x(千米)与计费y(元)之间的函数图象.
(1)由图象写出乘车里程为5千米时选择 (“顺风车”或“快车”)更便宜;
(2)当x>5时,顺风车的函数是y=![]() x+
x+![]() ,判断乘车,里程是8千米时,选择“顺风车”和“快车”哪个更便宜?说明理由.
,判断乘车,里程是8千米时,选择“顺风车”和“快车”哪个更便宜?说明理由.
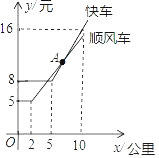
【答案】(1)快车(2)里程是8千米时,选择“顺风车”更便宜
【解析】
(1)观察函数图象,找出当x=5时费用更低的打车方式,此题得解;
(2)观察函数图象,找出点的坐标,利用待定系数法可求出当x>5时“快车”的函数关系式,再利用一次函数图象上点的坐标特征求出当x=8时两种打车方式所需费用,比较后即可得出结论.
(1)观察函数图象,可知:当x=5时,快车的费用更便宜.
故答案为:“快车”.
(2)设当x>5时,“快车”的函数关系式为y=kx+b(k≠0),
将(5,8),(10,16)代入y=kx+b,得:![]() ,
,
解得: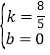 ,
,
∴当x>5时,“快车”的函数关系式为y=![]() x.
x.
当x=8时,y=![]() x+
x+![]() =
=![]() ;
;
当x=8时,y=![]() x=
x=![]() .
.
∵![]() <
<![]() ,
,
∴里程是8千米时,选择“顺风车”更便宜.


科目:初中数学 来源: 题型:
【题目】在关系式![]() 中有下列说法:①x是自变量,y是因变量;②x的数值可以任意选择;③y是变量,它的值与x无关;④用关系式表示的不能用图像表示;⑤y与x的关系还可以用列表法和图像法表示,其中说法正确的是( ).
中有下列说法:①x是自变量,y是因变量;②x的数值可以任意选择;③y是变量,它的值与x无关;④用关系式表示的不能用图像表示;⑤y与x的关系还可以用列表法和图像法表示,其中说法正确的是( ).
A.①②⑤B.①②④C.①③⑤D.①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一件工程甲独做50天可完,乙独做75天可完,现在两个人合作,但是中途乙因事离开几天,从开工后40天把这件工程做完,则乙中途离开了( )天.
A. 10 B. 20 C. 30 D. 25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC与△CDE都是等边三角形,点B、C、D在同一直线上,AD与BE相交于点G,BE与AC相交于点F,AD与CE相交于点H,则下列结论:①△ACD≌△BCE;②∠AGB=60°;③BF=AH;④△CFH是等边三角形;⑤连CG,则∠BGC=∠DGC ;⑥EG+GC=GD. 其中正确的有________.(只要写序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、E分别在直线AC和DF上,若∠AGB=∠EHF,∠C=∠D,可以证明
∠A=∠F.请完成下面证明过程中的各项“填空”
证明:∵∠AGB=∠EHF(已知)
∠AGB= (对顶角相等)
∴∠EHF=∠DGF(等量代换)
∴ ∥EC(理由: )
∴∠ =∠DBA(两直线平行,同位角相等)
又∵∠C=∠D,∴∠DBA= (等量代换)
∴DF∥ (内错角相等,两直线平行)
∴∠A=∠F(理由: )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(0,4)、C(﹣2,0)在直线l:y=kx+b上,l和函数y=﹣4x+a的图象交于点B
(1)求直线l的表达式;
(2)若点B的横坐标是1,求关于x、y的方程组![]() 的解及a的值.
的解及a的值.
(3)若点A关于x轴的对称点为P,求△PBC的面积.
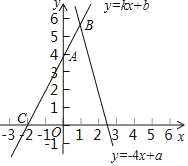
查看答案和解析>>
科目:初中数学 来源: 题型:
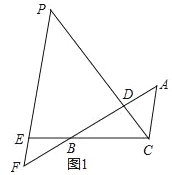
【题目】如图1,△ABC中,点D在线段AB上,点E在线段CB延长线上,且BE=CD,EP∥AC交直线CD于点P,交直线AB于点F,∠ADP=∠ACB.
(1)图1中是否存在与AC相等的线段?若存在,请找出,并加以证明,若不存在,说明理由;
(2)若将“点D在线段AB上,点E在线段CB延长线上”改为“点D在线段BA延长线上,点E在线段BC延长线上”,其他条件不变(如图2).当∠ABC=90°,∠BAC=60°,AB=2时,求线段PE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是长方形纸带,将纸带沿EF折叠成图2,再沿BF折叠成图3.
(1)若∠DEF=20°,则图3中∠CFE度数是多少?
(2)若∠DEF=a,把图3中∠CFE用a表示.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线l:y= ![]() (x﹣h)2﹣2与x轴交于A,B两点(点A在点B的左侧),将抛物线ι在x轴下方部分沿轴翻折,x轴上方的图象保持不变,就组成了函数的图象.
(x﹣h)2﹣2与x轴交于A,B两点(点A在点B的左侧),将抛物线ι在x轴下方部分沿轴翻折,x轴上方的图象保持不变,就组成了函数的图象.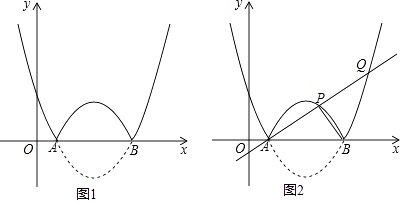
(1)若点A的坐标为(1,0).
①求抛物线l的表达式,并直接写出当x为何值时,函数的值y随x的增大而增大;
②如图2,若过A点的直线交函数的图象于另外两点P,Q,且S△ABQ=2S△ABP , 求点P的坐标;
(2)当2<x<3时,若函数f的值随x的增大而增大,直接写出h的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com