
����Ŀ����ͼ��������l��y= ![]() ��x��h��2��2��x�ύ��A��B���㣨��A�ڵ�B����ࣩ���������ߦ���x���·��������ᷭ�ۣ�x���Ϸ���ͼ�ֲ��䣬������˺�����ͼ��
��x��h��2��2��x�ύ��A��B���㣨��A�ڵ�B����ࣩ���������ߦ���x���·��������ᷭ�ۣ�x���Ϸ���ͼ�ֲ��䣬������˺�����ͼ��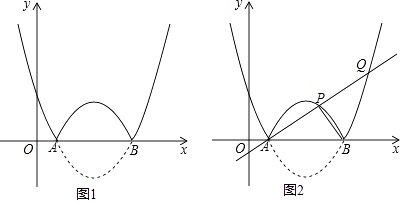
��1������A��������1��0����
����������l�ı���ʽ����ֱ��д����xΪ��ֵʱ��������ֵy��x�����������
����ͼ2������A���ֱ�߽�������ͼ������������P��Q����S��ABQ=2S��ABP �� ���P�����ꣻ
��2����2��x��3ʱ��������f��ֵ��x�����������ֱ��д��h��ȡֵ��Χ��
���𰸡�
��1���⣺�ٰ�A��1��0������������y= ![]() ��x��h��2��2�еã�
��x��h��2��2�еã�
![]() ��x��h��2��2=0��
��x��h��2��2=0��
��ã�h=3��h=��1��
�ߵ�A�ڵ�B����࣬
��h��0��
��h=3��
��������l�ı���ʽΪ��y= ![]() ��x��3��2��2��
��x��3��2��2��
�������ߵĶԳ����ǣ�ֱ��x=3��
�ɶԳ��Եã�B��5��0����
��ͼ���֪����1��x��3��x��5ʱ��������ֵy��x�����������
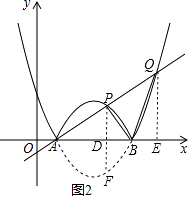
����ͼ2����PD��x���ڵ�D���ӳ�PD��������l�ڵ�F����QE��x����E����PD��QE��
�ɶԳ��Եã�DF=PD��
��S��ABQ=2S��ABP��
�� ![]() ABQE=2��
ABQE=2�� ![]() ABPD��
ABPD��
��QE=2PD��
��PD��QE��
���PAD�ס�QAE��
�� ![]() ��
��
��AE=2AD��
��AD=a����OD=1+a��OE=1+2a��P��1+a����[ ![]() ��1+a��3��2��2]����
��1+a��3��2��2]����
�ߵ�F��Q��������l�ϣ�
��PD=DF=��[ ![]() ��1+a��3��2��2]��
��1+a��3��2��2]��
QE= ![]() ��1+2a��3��2��2��
��1+2a��3��2��2��
�� ![]() ��1+2a��3��2��2=��2[
��1+2a��3��2��2=��2[ ![]() ��1+a��3��2��2]��
��1+a��3��2��2]��
��ã�a= ![]() ��a=0���ᣩ��
��a=0���ᣩ��
��P�� ![]() ��
�� ![]() ��
��
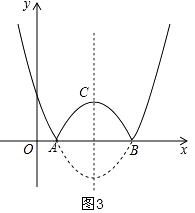
��2���⣺��y=0ʱ�� ![]() ��x��h��2��2=0��
��x��h��2��2=0��
��ã�x=h+2��h��2��
�ߵ�A�ڵ�B����࣬��h��0��
��A��h��2��0����B��h+2��0����
��ͼ3���������ߵĶԳ��ύ�������ڵ�C��
�����������
����ͼ���֪��ͼ��f��AC��ʱ������f��ֵ��x�����������
�� ![]() ��
��
��3��h��4��
����ͼ���֪��ͼ��f��B���Ҳ�ʱ������f��ֵ��x�����������
����h+2��2��
h��0��
������������3��h��4��h��0ʱ������f��ֵ��x�����������
����������1�������ô���ϵ�����������ߵĽ���ʽ���ɶԳ������B�����꣬����ͼ��д��������ֵy��x��������������������ƣ���x��ȡֵ������ͼ2���������ߣ������ԳƵ�F��ֱ�ǽ�������AQE������S��ABQ=2S��ABP����QE=2PD��֤����PAD�ס�QAE���� ![]() ����AE=2AD����AD=a������QE=2FD�з��̿����a��ֵ��������P�����ꣻ��2������y=0����������x��������������꣬����ͼ���г��������ƵIJ��֣��������֣��ֱ����ۣ����в���ʽ��ʽ��ɵ�h��ȡֵ��
����AE=2AD����AD=a������QE=2FD�з��̿����a��ֵ��������P�����ꣻ��2������y=0����������x��������������꣬����ͼ���г��������ƵIJ��֣��������֣��ֱ����ۣ����в���ʽ��ʽ��ɵ�h��ȡֵ��
�����㾫�������ն��κ����������ǽ����ĸ�������Ҫ֪�������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
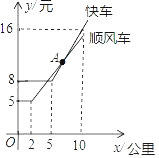
����Ŀ����ͼ��ʾij��˾��˳�糵���롰�쳵������ʻ���x��ǧ�ף���Ʒ�y��Ԫ��֮��ĺ���ͼ��
��1����ͼ��д���˳����Ϊ5ǧ��ʱѡ���� ������˳�糵���쳵���������ˣ�
��2����x��5ʱ��˳�糵�ĺ�����y��![]() x+
x+![]() ���жϳ˳��������8ǧ��ʱ��ѡ��˳�糵���͡��쳵���ĸ������ˣ�˵�����ɣ�
���жϳ˳��������8ǧ��ʱ��ѡ��˳�糵���͡��쳵���ĸ������ˣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OABC�ı�OA��x���ϣ�AC��OB���ڵ�D ��8��4��������������y= ![]() ��ͼ����D����������OABC����ƽ��n����λ��ʹ��C���ڸ÷���������ͼ���ϣ���n��ֵΪ ��
��ͼ����D����������OABC����ƽ��n����λ��ʹ��C���ڸ÷���������ͼ���ϣ���n��ֵΪ �� 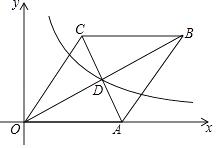
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
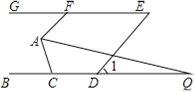
����Ŀ����ͼ����֪BC��GE��AF��DE����D��ֱ��BC�ϣ���F��ֱ��GE�ϣ��ҡ�1=50����
��1�����AFG�Ķ�����
��2����AQƽ�֡�FAC����ֱ��BC�ڵ�Q���ҡ�Q=18�������ACB�Ķ���Ϊ______������ֱ��д���𰸣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��A��B��C�Dz���ͬһ��ֱ���ϵ����㣬�밴����Ҫ��ͼ������(��ͼʱ���߲���,����д������,ֻ�軭��ͼ�Ρ���ע��ĸ):
(1)��ֱ��BC,����AC��
(2)���߶�BC���е�D,����AD��
(3)������ADC��ƽ���߽�AC�ڵ�E��
(4)����BDA=![]() ���ADC����EDC.
���ADC����EDC.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
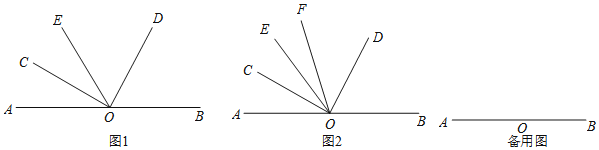
����Ŀ����OΪֱ��AB��һ�㣬��ֱ��AB�ϲ�����һ����COD��ʹ�á�COD=90����
��1����ͼ1������O������OE����OEǡ��Ϊ��AOD�Ľ�ƽ����ʱ����ֱ��д����BOD���COE֮��ı�����ϵ������BOD= ______ ��COE����һ�����֣���
��2����ͼ2������O������OE����OCǡ��Ϊ��AOE�Ľ�ƽ����ʱ����������OF��ʹ��OFƽ�֡�COD�����FOB+��EOC�Ķ�����
��3���ڣ�2���������£�����EOC=3��EOF�����AOE�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
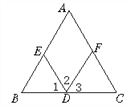
����Ŀ����ͼ��(1)�ߡ�A=_____(��֪)��
��AC��ED( )
(2)�ߡ�2=_____(��֪)��
��AC��ED( )
(3)�ߡ�A+_____=180��(��֪)��
��AB��FD( )
(4)��AB��_____(��֪)��
���2+��AED=180��( )
(5)��AC��_____(��֪)��
���C=��1( )
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�ܳ�2.5������AB��ͼ��ʾб����һ��ǽ�ϣ���ʱ����B��ǽ��C����C��90�㣩�ľ���BCΪ0.7�ף�
��1�����ʱ�ݶ�A�����ĸ߶�AC��
��2������ݶ�A�»�0��9�ף���ô����B��ˮƽ�������һ����˶����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ҷ��˹�ͬ����2��a+x��(b+x),���ڼ׳����˵�һ������ʽ��a�ķ��ţ��õ����Ϊ![]() �������ҳ�©��2���õ��Ľ��Ϊ
�������ҳ�©��2���õ��Ľ��Ϊ![]()
��1����a��b��ֵ ;
��2�������ȷ�Ľ��.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com