
【题目】如图,已知△ABC与△CDE都是等边三角形,点B、C、D在同一直线上,AD与BE相交于点G,BE与AC相交于点F,AD与CE相交于点H,则下列结论:①△ACD≌△BCE;②∠AGB=60°;③BF=AH;④△CFH是等边三角形;⑤连CG,则∠BGC=∠DGC ;⑥EG+GC=GD. 其中正确的有________.(只要写序号)

【答案】①②③④⑤⑥
【解析】
利用等边三角形的性质得出条件,可证明:△BCE≌△ACD;利用△BCE≌△ACD得出∠CBF=∠CAH,再运用平角定义得出∠BCF=∠ACH,进而得出△BCF≌△ACH因此BF=AH.由CF=CH和∠ACH=60°根据“有一个角是60°的三角形是等边三角形可得△CFH是等边三角形.连接CG,过C作CI⊥BE于I,CJ⊥AD于J.由全等三角形对应边上的高相等得到CI=CJ,由角平分线的判定定理得到GC平分∠BGD.
在GD上截取GM=GE,连接EM.由∠EGM=∠AGB=60°,得到△EGM是等边三角形,得到ME=GE,∠GEM=60°.通过证明△GEC≌△MED,得到GC=MD,即可得到GD=GM+MD=GE+CG.
∵∠BCA=∠DCE=60°,∴∠ACE=60°,∴∠BCE=∠ACD.在△BCE和△ACD中,∵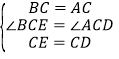 ,∴△BCE≌△ACD(SAS);故①正确;
,∴△BCE≌△ACD(SAS);故①正确;
∵△BCE≌△ACD,∴∠CBF=∠CAH.
∵∠BFC=∠AFG,∴∠AGB=∠ACB=60°,故②正确;
在△BCF和△ACH中,∵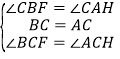 ,∴△BCF≌△ACH(ASA),∴CF=CH,BF=AH;故③正确;
,∴△BCF≌△ACH(ASA),∴CF=CH,BF=AH;故③正确;
∵CF=CH,∠ACH=60°,∴△CFH是等边三角形;故④正确;
连接CG.过C作CI⊥BE于I,CJ⊥AD于J.
∵△BCE≌△ACD,∴CI=CJ,∴GC平分∠BGD,∴∠BGC=∠DGC.故⑤正确.
在GD上截取GM=GE,连接EM.
∵∠EGM=∠AGB=60°,∴△EGM是等边三角形,∴ME=GE,∠GEM=60°.
∵∠CED=60°,∴∠GEC=∠MED.在△GEC和△MED中,∵GE=ME ,∠GEC=∠MED,CE=DE,∴△GEC≌△MED,∴GC=MD,∴GD=GM+MD=GE+CG.故⑥正确.
故答案为:①②③④⑤⑥.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】七年级(2)班的同学组织到人民公园游玩,张明、王励、李华三位同学和其他同学走散了,同学们已到中心广场,他们三个对着景区示意图在电话中向在中心广场的同学们说他们的位置,张明说他的坐标是![]() ,王励说他的坐标是
,王励说他的坐标是![]() ,李华说他的坐标是
,李华说他的坐标是![]() .
.
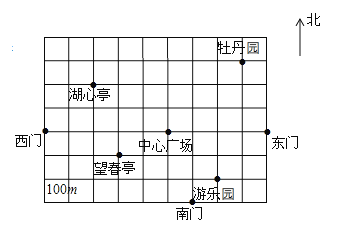
(1)请你根据题目条件,在图中画出平面直角坐标系;
(2)写出这三位同学所在的位置;
(3)写出除了这三位同学所在位置外,图中其余两个景点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是某公共汽车线路收支差额y(票价总收入减去运营成本)与乘客量x的函数图象,目前这条线路亏损,为了扭亏,有关部门举行提高票价的听证会,乘客代表认为:公交公司应降低运营成本,实现扭亏,公交公司认为:运营成本难以下降,提高票价才能扭亏根据这两种意见,把图①分别改画成图②和图③.则下列判断不合理的是( )

A. 图①中点A的实际意义是公交公司运营后亏损1万元
B. 图①中点B的实际意义是乘客量为1.5万时公交公司收支平衡
C. 图②能反映公交公司意见
D. 图③能反映乘客意见
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点P从点A出发,沿着正方形的边顺时针方向运动一周,则△APC的面积y与点P运动的路程x之间形成的函数关系图象大致是( )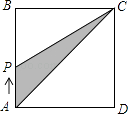
A.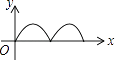
B.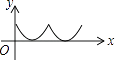
C.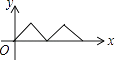
D.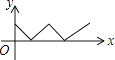
查看答案和解析>>
科目:初中数学 来源: 题型:
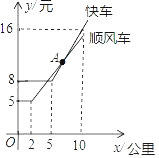
【题目】如图表示某公司“顺风车”与“快车”的行驶里程x(千米)与计费y(元)之间的函数图象.
(1)由图象写出乘车里程为5千米时选择 (“顺风车”或“快车”)更便宜;
(2)当x>5时,顺风车的函数是y=![]() x+
x+![]() ,判断乘车,里程是8千米时,选择“顺风车”和“快车”哪个更便宜?说明理由.
,判断乘车,里程是8千米时,选择“顺风车”和“快车”哪个更便宜?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表中有两种移动电话计费方式:
月使用费(元) | 主叫限定时间(分钟) | 主叫超时费(元/分钟) | 被叫 | |
方式一 | 65 | 160 | 0.25 | 免费 |
方式二 | 100 | 380 | 0.19 | 免费 |
说明:月使用费固定收取,主叫不超限定时间不再收费,主叫超时部分加收超时费;被叫免费.
(1)若李杰某月主叫通话时间为200分钟则他按方式一计费需 元,按方式二计费需 元;若他按方式二计费需103.8元,则主叫通话时间为 分钟;
(2)是否存在某主叫通话时间t(分钟),按方式一和方式二的计费相等,若存在,请求出t的值;若不存在,请说明理由;
(3)请你通过计算分析后,直接给出当月主叫通话时间t(分钟)满足什么条件时,选择方式一省钱;当每月主叫通话时间t(分钟)满足什么条件时,选择方式二省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
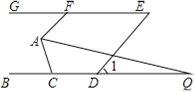
【题目】如图,已知BC∥GE,AF∥DE,点D在直线BC上,点F在直线GE上,且∠1=50°.
(1)求∠AFG的度数;
(2)若AQ平分∠FAC,交直线BC于点Q,且∠Q=18°,则∠ACB的度数为______°.(直接写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com