
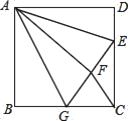
【题目】如图,正方形ABCD中,AB=12,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论: ①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=28.8. 其中正确结论的个数是( )
A. 4 B. 3 C. 2 D. 1
【答案】B
【解析】
由正方形的性质和折叠的性质得出AB=AF,∠AFG=90°,由HL证明Rt△ABG≌Rt△AFG,得出①正确;
设BG=FG=x,则CG=12﹣x.由勾股定理得出方程,解方程求出BG,得出GC,即可得出②正确;
由全等三角形的性质和三角形内角和定理得出∠AGB=∠GCF,得出AG∥CF,即可得出③正确;
通过计算三角形的面积得出④错误;即可得出结果.
①正确.理由如下:
∵四边形ABCD是正方形,∴AB=BC=CD=AD=12,∠B=∠GCE=∠D=90°,由折叠的性质得:AF=AD,∠AFE=∠D=90°,∴∠AFG=90°,AB=AF.在Rt△ABG和Rt△AFG中,![]() ,∴Rt△ABG≌Rt△AFG(HL);
,∴Rt△ABG≌Rt△AFG(HL);
②正确.理由如下:
由题意得:EF=DE=![]() CD=4,设BG=FG=x,则CG=12﹣x.
CD=4,设BG=FG=x,则CG=12﹣x.
在直角△ECG中,根据勾股定理,得(12﹣x)2+82=(x+4)2,解得:x=6,∴BG=6,∴GC=12﹣6=6,∴BG=GC;
③正确.理由如下:
∵CG=BG,BG=GF,∴CG=GF,∴△FGC是等腰三角形,∠GFC=∠GCF.
又∵Rt△ABG≌Rt△AFG,∴∠AGB=∠AGF,∠AGB+∠AGF=2∠AGB=180°﹣∠FGC=∠GFC+∠GCF=2∠GFC=2∠GCF,∴∠AGB=∠GCF,∴AG∥CF;
④错误.理由如下:
∵S△GCE=![]() GCCE=
GCCE=![]() ×6×8=24.
×6×8=24.
∵GF=6,EF=4,△GFC和△FCE等高,∴S△GFC:S△FCE=3:2,∴S△GFC=![]() ×24=
×24=![]() ≠28.8.
≠28.8.
故④不正确,∴正确的有①②③.
故选B.


科目:初中数学 来源: 题型:
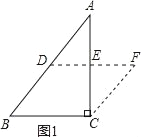
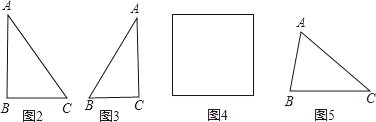
【题目】在△ABC中,沿图示的中位线DE剪一刀,拼成如图1所示的平行四边形BCFD.请仿上述方法,按要求完成下列操作设计,并在规定位置画出图示:
(1)在△ABC中,若∠C=90°,沿着中位线剪一刀,可拼成矩形或等腰梯形,请将拼成的图形画在图2位置(只需画一个);
(2)在△ABC中,若AB=2BC,沿着中位线剪一刀,可拼成菱形,并将拼成的图形画在图3位置;
(3)在△ABC中,需增加什么条件,沿着中位线剪一刀,拼成正方形,并将拼成的图形和符合条件的三角形一同画在图4位置;
(4)在△ABC中,若沿着某条线剪一刀,能拼成等腰梯形,请将拼成的图形画在图5位置(保留寻求剪裁线的痕迹).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+4与x轴交于A(﹣2,0)、B(4、0)两点,与y轴交于C点.
(1)求抛物线的解析式;
(2)T是抛物线对称轴上的一点,且△ATC是以AC为底的等腰三角形,求点T的坐标;
(3)M、Q两点分别从A、B点以每秒1个单位长度的速度沿x轴同时出发相向而行,当点M到原点时,点Q立刻掉头并以每秒 ![]() 个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动,过点M的直线l⊥x轴交AC或BC于点P.求点M的运动时间t与△APQ面积S的函数关系式,并求出S的最大值.
个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动,过点M的直线l⊥x轴交AC或BC于点P.求点M的运动时间t与△APQ面积S的函数关系式,并求出S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察:从2开始,连续的偶数相加,它们的和的情况如下图:

(1)当加数m的个数为n时,和(S)与n之间有什么样的数量关系,用公式表示出来;
(2)按此规律计算(写出必要的演算过程):
①2+4+6+…+300的值;
②162+164+166+…+400的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,P(a,b)是△ABC的边AC上一点,△ABC经平移得到△A1B1C1,且点P的对应点为P1(a+5,b+4).
(1)写出△ABC的三个顶点的坐标;
(2)请在平面直角坐标系中画出△A1B1C1.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC边上的垂直平分线交AC于D,交AB于E,延长DE到F,使BF=CE
(1)四边形BCEF是平行四边形吗?说说你的理由.
(2)当∠A等于多少时,四边形BCEF是菱形,并说出你的理由.
(3)四边形BCEF可以是正方形吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
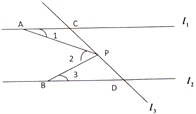
【题目】如图,已知直线![]() ,直线
,直线![]() 和直线交于点
和直线交于点![]() 和点
和点![]() ,
,![]() 为直线
为直线![]() 上的一点,
上的一点,![]() ,
,![]() 分别是直线
分别是直线![]() ,
,![]() 上的定点.
上的定点.
(1)若![]() 点在线段
点在线段![]() (
(![]() 、
、![]() 两点除外)上运动时,问
两点除外)上运动时,问![]() 、
、![]() 、
、![]() 之间的关系是什么?这种关系是否发生变化?请说明理由;
之间的关系是什么?这种关系是否发生变化?请说明理由;
(2)若![]() 在线段
在线段![]() 之外时,
之外时,![]() 、
、![]() 、
、![]() 的关系又怎样?说明理由.
的关系又怎样?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BF为⊙O的直径,直线AC交⊙O于A,B两点,点D在⊙O上,BD平分∠OBC,DE⊥AC于点E.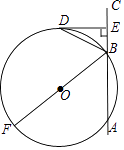
(1)求证:直线DE是⊙O的切线;
(2)若 BF=10,sin∠BDE= ![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com