
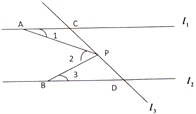
【题目】如图,已知直线![]() ,直线
,直线![]() 和直线交于点
和直线交于点![]() 和点
和点![]() ,
,![]() 为直线
为直线![]() 上的一点,
上的一点,![]() ,
,![]() 分别是直线
分别是直线![]() ,
,![]() 上的定点.
上的定点.
(1)若![]() 点在线段
点在线段![]() (
(![]() 、
、![]() 两点除外)上运动时,问
两点除外)上运动时,问![]() 、
、![]() 、
、![]() 之间的关系是什么?这种关系是否发生变化?请说明理由;
之间的关系是什么?这种关系是否发生变化?请说明理由;
(2)若![]() 在线段
在线段![]() 之外时,
之外时,![]() 、
、![]() 、
、![]() 的关系又怎样?说明理由.
的关系又怎样?说明理由.
【答案】(1)![]() ,不变化,理由见解析;(2)在
,不变化,理由见解析;(2)在![]() 上面时,
上面时,![]() ,在
,在![]() 下面时,
下面时,![]() ,理由见解析.
,理由见解析.
【解析】
(1)过点P作PE∥l1,根据l1∥l2可知PE∥l2,故可得出∠1=∠APE,∠3=∠BPE.再由∠2=∠APE+∠BPE即可得出结论;
(2)由于点P的位置不确定,故应分当点P在![]() 上面时与点P在
上面时与点P在![]() 下面时两种情况进行讨论.
下面时两种情况进行讨论.
(1)∠2=∠1+∠3.
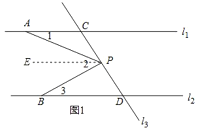
证明:如图1,过点P作PE∥l1,
∵l1∥l2,
∴PE∥l2,
∴∠1=∠APE,∠3=∠BPE.
又∵∠2=∠APE+∠BPE,
∴∠2=∠1+∠3;
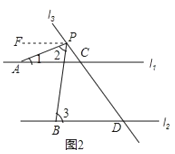
(2)①如图2所示,当点P在![]() 上面时,∠2=∠3∠1,
上面时,∠2=∠3∠1,
理由:过点P作PF∥l1,∠FPA=∠1.
∵l1∥l2,
∴PF∥l2,
∴∠FPB=∠3,
∴∠2=∠FPB∠PFA=∠3∠1;
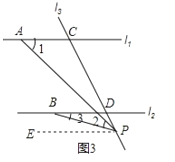
②如图3所示,当点P在![]() 下面时,∠2=∠1∠3,
下面时,∠2=∠1∠3,
理由:过点P作PE∥l2,∠EPB=∠3.
∵l1∥l2,
∴PE∥l1,
∴∠EPA=∠1,
∴∠2=∠EPA∠EPB=∠1∠3.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】观察如图所示的长方体.

(1)用符号表示下列两棱的位置关系:AB___A′B′,AA′_____AB,D′A′_____D′C′,AD______BC.
(2) A′B′与BC所在的直线是两条不相交的直线,它们_____平行线.(填“是”或“不是”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=12,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论: ①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=28.8. 其中正确结论的个数是( )
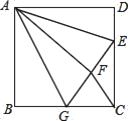
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为建设资源节约型、环境友好型社会,克服因干旱而造成的电力紧张困难,切实做好节能减排工作.某地决定对居民家庭用电实行“阶梯电价”,电力公司规定:居民家庭每月用电量在80千瓦时以下(含80千瓦时,1千瓦时俗称1度)时,实行“基本电价”;当居民家庭月用电量超过80千瓦时时,超过部分实行“提高电价”.
(1)小张家今年2月份用电100千瓦时,上缴电费68元;5月份用电120千瓦时,上缴电费88元.求“基本电价”和“提高电价”分别为多少元/千瓦时;
(2)若6月份小张家预计用电130千瓦时,请预算小张家6月份应上缴的电费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如下图, AB∥CD,点E,F分别为AB,CD上一点.
(1) 在AB,CD之间有一点M(点M不在线段EF上),连接ME,MF,试探究∠AEM,∠EMF,∠MFC之间有怎样的数量关系. 请补全图形,并在图形下面写出相应的数量关系,选其中一个进行证明.

(2)如下图,在AB,CD之间有两点M,N,连接ME,MN,NF,请选择一个图形写出∠AEM,∠EMN,∠MNF,∠NFC 存在的数量关系(不需证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,长方形ABCD中,AB=8,BC=10,在边CD上取一点E,将△ADE折叠后点D恰好落在BC边上的点F.
(1)求CE的长;
(2)建立平面直角坐标系如图②所示,在x轴上找一点P,使PA+PE的值最小,求出最小值和点P的坐标;
(3)如图③,DE的延长线与AF的延长线交于点G,在y轴上是否存在点M,使△FGM是直角三角形?如果存在,求出点M的坐标:如果不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OE⊥AB于O,若∠BOD=40°,则不正确的结论是( )

A.∠AOC=40° B.∠COE=130° C.∠EOD=40° D.∠BOE=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在10×10的正方形网格中(每个小正方形的边长都为1个单位),△ABC的三个顶点都在格点上.建立如图所示的直角坐标系,
(1)请在图中标出△ABC的外接圆的圆心P的位置,并填写: 圆心P的坐标:P( , )
(2)将△ABC绕点A逆时针旋转90°得到△ADE,画出图形,并求△ABC扫过的图形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com