
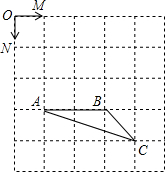
 如图,已知正方形网格中每个小正方形的边长为1,点O、M、N、A、B、C都是小正方形的顶点.
如图,已知正方形网格中每个小正方形的边长为1,点O、M、N、A、B、C都是小正方形的顶点.分析 (1)根据平行四边形法则作向量$\overrightarrow{BD}=2\overrightarrow a-2\overrightarrow b$,小正方形的两条对角线的长度即为所求;
(2)由图可知△ABC和△DAB各边的长,根据三角形三边对应成比例证明相似;
(3)由图可知∠ABD=90°+45°=135°,借助于相似三角形(△ABD∽△CBA)的性质来计算.
解答 (1)解:作向量$\overrightarrow{BD}=2\overrightarrow a-2\overrightarrow b$,
$|{\overrightarrow{BD}}|$=2$\sqrt{2}$,
故答案为:2$\sqrt{2}$;
(2)证明:∵$\frac{BC}{AB}=\frac{{\sqrt{2}}}{2},\frac{AB}{BD}=\frac{2}{{2\sqrt{2}}}=\frac{{\sqrt{2}}}{2},\frac{AC}{AD}=\frac{{\sqrt{10}}}{{2\sqrt{5}}}=\frac{{\sqrt{2}}}{2}$,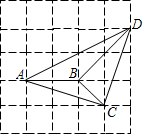
∴$\frac{BC}{AB}=\frac{AB}{BD}=\frac{AC}{AD}$,
∴△ABC∽△DAB;
(3)解:由图可知∠ABD=90°+45°=135°,
故答案为:135°;
∵AC=CD=$\sqrt{10}$,
∴∠CAD=∠CDA,
又△ABD∽△CBA,
∴∠ADB=∠CAB,
∴∠CAD-∠CAB=∠CDA-∠ADB,
即∠BAD=∠BDC,
∵∠BAD=∠BCA,
∴∠BDC=∠ACB.
点评 本题主要考查了平面向量、相似三角形的判定与性质,根据正方形网格中每个小正方形的边长为1,算出各线段的长度是解答此题的关键.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
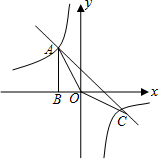 如图,Rt△ABO的顶点A是双曲线y=$\frac{k}{x}$(k≠0)与直线y=-x-(k+1)在第二象限的交点,AB⊥x轴于B,点C是双曲线与直线的另一个交点,且S△ABO=$\frac{3}{2}$.
如图,Rt△ABO的顶点A是双曲线y=$\frac{k}{x}$(k≠0)与直线y=-x-(k+1)在第二象限的交点,AB⊥x轴于B,点C是双曲线与直线的另一个交点,且S△ABO=$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com