
分析 (1)移项得x2=-5,根据阅读材料求出x=±$\sqrt{5}$i;
(2)先将原式配方后变为(x+$\frac{1}{2}$)2=-$\frac{3}{4}$,再将x+$\frac{1}{2}$当作一个整体按照条件中的方法就可以求出其值.
解答 解:(1)x2+5=0,
x2=-5,
x=±$\sqrt{5}$i,
x1=$\sqrt{5}$i,x2=-$\sqrt{5}$i;
(2)原方程变形为:(x+$\frac{1}{2}$)2=-$\frac{3}{4}$,
∴x+$\frac{1}{2}$=±$\frac{\sqrt{3}}{2}$i,
∴x1=-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i,x2=-$\frac{1}{2}$-$\frac{\sqrt{3}}{2}$i.
点评 本题考查了一元二次方程的运用以及解法,在解答中要求学生具有较强的阅读能力和分析能力,解决现实生活中的实际问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2015-2016学年内蒙古巴彦淖尔市临河区七年级下学期期末考试数学试卷(解析版) 题型:判断题
为奖励在文艺汇演中表现突出的同学,班主任派生活委员小亮到文具店为获奖同学购买奖品.小亮发现,如果买1个笔记本和3支钢笔,则需要18元;如果买2个笔记本和5支钢笔,则需要31元.
(1)求购买每个笔记本和每支钢笔各多少元?
(2)班主任给小亮的班费是100元,需要奖励的同学是24名(每人奖励一件奖品),若购买的钢笔数不少于笔记本数,小亮最多能买多少个笔记本?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
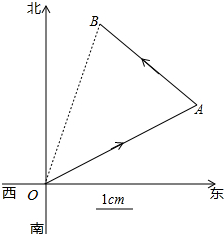 如图,一只蚂蚁从点O出发,沿北偏东60°方向爬行4cm后到达A地,后折向西北方向爬行3cm到达B点.
如图,一只蚂蚁从点O出发,沿北偏东60°方向爬行4cm后到达A地,后折向西北方向爬行3cm到达B点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
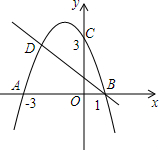 如图,二次函数的图象与x轴相交于A(-3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
如图,二次函数的图象与x轴相交于A(-3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
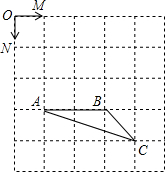 如图,已知正方形网格中每个小正方形的边长为1,点O、M、N、A、B、C都是小正方形的顶点.
如图,已知正方形网格中每个小正方形的边长为1,点O、M、N、A、B、C都是小正方形的顶点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 相交 | B. | 相切 | C. | 相交或相离 | D. | 相离 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com