
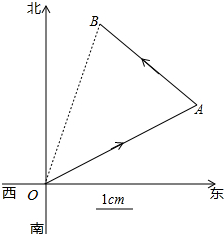
 如图,一只蚂蚁从点O出发,沿北偏东60°方向爬行4cm后到达A地,后折向西北方向爬行3cm到达B点.
如图,一只蚂蚁从点O出发,沿北偏东60°方向爬行4cm后到达A地,后折向西北方向爬行3cm到达B点.科目:初中数学 来源:2017届江苏省东台市第四教育联盟九年级下学期第一次月考数学试卷(解析版) 题型:单选题
下列命题错误的是( )
A. 平行四边形的对角线互相平分 B. 矩形的对角线相等
C. 对角线互相垂直平分的四边形是菱形 D. 对角线相等的四边形是矩形
查看答案和解析>>
科目:初中数学 来源:2015-2016学年内蒙古巴彦淖尔市临河区七年级下学期期末考试数学试卷(解析版) 题型:单选题
已知:关于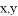 的方程组
的方程组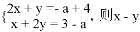 的值为( )
的值为( )
A. -1 B. 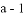 C. 0 D. 1
C. 0 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
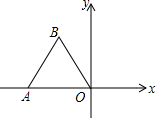 如图,△OAB是边长为2的等边三角形.
如图,△OAB是边长为2的等边三角形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com