
【题目】如图,抛物线y=ax2﹣x+4与x轴交于点A,B,B点的坐标为(﹣4,0),与y轴交于点C.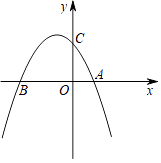
(1)求抛物线的解析式和对称轴.
(2)连接AC、BC,在x轴下方的抛物线上求一点M,使△ABM与△ABC的面积相等.
(3)在x轴下方作平行于x轴的直线l,与抛物线交于点D、E两点(点D在对称轴的左侧).过点D、E分别作x轴的垂线,垂足分别为G、F,当矩形DEFG中DE=2DG时,求D点的坐标.
【答案】
(1)解:把B(﹣4,0)代入y=ax2﹣x+4得16a+4+4=0,解得a=﹣ ![]() ,
,
所以抛物线的解析式为y=﹣ ![]() x2﹣x+4,
x2﹣x+4,
抛物线的对称轴为直线x=﹣ ![]() =﹣1
=﹣1
(2)解:当x=0时,y=﹣ ![]() x2﹣x+4=4,则C(0,4),
x2﹣x+4=4,则C(0,4),
∵△ABM与△ABC的面积相等,
∴点M的纵坐标为﹣4,
当y=﹣4时,﹣ ![]() x2﹣x+4=﹣4,解得x1=﹣1+
x2﹣x+4=﹣4,解得x1=﹣1+ ![]() ,x2=﹣1﹣
,x2=﹣1﹣ ![]() ,
,
∴M点的坐标为(﹣1+ ![]() ,﹣4)或(﹣1﹣
,﹣4)或(﹣1﹣ ![]() ,﹣4)
,﹣4)
(3)解:如图, 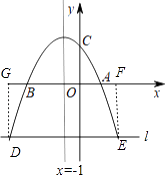
设D(t,﹣ ![]() t2﹣t+4)(t<﹣1)
t2﹣t+4)(t<﹣1)
∵DE=2DG,
∴﹣1﹣t=﹣(﹣ ![]() t2﹣t+4),
t2﹣t+4),
整理得t2+4t﹣6=0,解得t1=﹣2﹣ ![]() ,t2=﹣2+
,t2=﹣2+ ![]() ,
,
∴D(﹣2﹣ ![]() ,﹣1﹣
,﹣1﹣ ![]() ).
).
【解析】(1)B点在抛物线上,故此点B的坐标符合抛物线的函数解析式,将点B的坐标代入函数关系式可求得a的值;
(2)将x=0代入抛物线的解析式求得对应的y的值,从而可得到点C的坐标,再利用三角形面积公式得到点M、C点到x轴的距离相等,即点M的纵坐标为-4,然后解方程-![]() ,x2-x+4=-4即可得到M点的坐标;
,x2-x+4=-4即可得到M点的坐标;
(3)设D(t,-![]() t2-t+4)(t<-1),利用DE=2DG和抛物线的对称性得到关于t的方程,从而可求得t的值,故此可得到点D的坐标.
t2-t+4)(t<-1),利用DE=2DG和抛物线的对称性得到关于t的方程,从而可求得t的值,故此可得到点D的坐标.


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H,将△ADF绕点A顺时针旋转90°得到△ABG,若BE=2,DF=3,则AH的长为 . 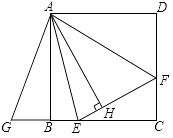
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接体育中考,某校九年级开展了体育中考项目的第一次模拟测验. 下图为某校九年级同学各项目达标人数统计图: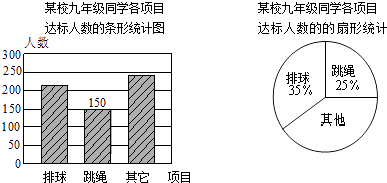
(1)在九年级学生中,达标的总人数是;
(2)在扇形统计图中,表示“其他”项目扇形的圆心角的度数是;
(3)经过一段时间的练习,在第二次模拟测验中,“排球”项目达标的人数增长到了231人,则“排球”项目达标人数的增长率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
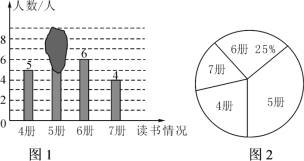
【题目】老师随机抽查了本学期学生读课外书册数的情况,绘制成条形统计图(如图1)和不完整的扇形图(如图2),其中条形统计图被墨迹遮盖了一部分.
(1)求条形统计图中被遮盖的数,并写出册数的中位数;
(2)随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没有改变,则最多补查了____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场准备进一批两种不同型号的衣服,已知购进![]() 种型号衣服9件,
种型号衣服9件,![]() 种型号衣服10件,则共需1810元;若购进
种型号衣服10件,则共需1810元;若购进![]() 种型号衣服12件,
种型号衣服12件,![]() 种型号衣服8件,共需1880元;已知销售一件
种型号衣服8件,共需1880元;已知销售一件![]() 型号衣服可获利18元,销售一件
型号衣服可获利18元,销售一件![]() 型号衣服可获利30元.要使在这次销售中获利不少于699元,且
型号衣服可获利30元.要使在这次销售中获利不少于699元,且![]() 型号衣服不多于28件.
型号衣服不多于28件.
(1)求![]() 型号衣服进价各是多少元?
型号衣服进价各是多少元?
(2)若已知购进![]() 型号衣服是
型号衣服是![]() 型号衣服的2倍还多4件,则商店在这次进货中可有几种方案?并简述购货方案.
型号衣服的2倍还多4件,则商店在这次进货中可有几种方案?并简述购货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AB=13,AC=12,经过点C且与AB边相切的动圆与BC、CA分别相交于点M、N,则线段MN长度的最小值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列每对数在数轴上的对应点间的距离,3与5,6与-2,-4与3,-2与-6.并回答下列各题:
(1)若数轴上的点A表示的数为6,点B表示的数为-2,则A与B两点间的距离是_______;
(2)若数轴上的点A表示的数为x,点B表示的数为3,则A与B两点间的距离可以表示为________(用含x的代数式表示);
(3)若数轴上的点A表示的数为x,结合数轴可求得|x+4|+|x-2|的最小值为______,取得最小值时x的取值范围为________;
(4)满足|x+4|+|x-2|>6的x的取值范围为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一水池放水,先用一台抽水机工作一段时间后停止,然后再调来一台同型号抽水机,两台抽水机同时工作直到抽干.设从开始工作的时间为![]() ,剩下的水量为
,剩下的水量为![]() .下面能反映
.下面能反映![]() 与
与![]() 之间的关系的大致图象是( )
之间的关系的大致图象是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com